Next: Estimating the inverse gradient
Up: VESUVIUS PHASE UNWRAPPING
Previous: VESUVIUS PHASE UNWRAPPING
curl grad
The relation (76) between the phases and the phase differences is
| ![\begin{displaymath}
\left[
\begin{array}
{rrrr}
-1 & 1& 0& 0 \\ 0 & 0& -1& 1 ...
... \\ \Delta \phi_{ac} \\ \Delta \phi_{bd}
\end{array}\right]\end{displaymath}](img189.gif) |
(77) |
Starting from the phase differences,
equation (77) cannot find all the phases themselves
because an additive constant cannot be found.
In other words,
the column vector [1,1,1,1]' is in the null space.
Likewise, if we add phase increments while we move around a loop,
the sum should be zero.
Let the loop be
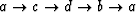 .The phase increments that sum to zero are:
.The phase increments that sum to zero are:
| 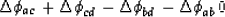 |
(78) |
Rearranging to agree with the order in equation (77) yields
| 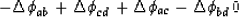 |
(79) |
which says that the row vector [-1,+1,+1,-1]
premultiplies (77),
yielding zero.
Rearrange again
| 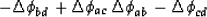 |
(80) |
and finally interchange signs and directions
(i.e., 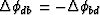 )
)
| 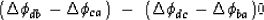 |
(81) |
This is the finite-difference equivalent of
| 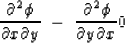 |
(82) |
and is also
the z-component of the theorem that the curl of a gradient
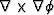 vanishes for any
vanishes for any 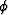 .
.
The four 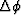 summed around the
summed around the 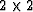 mesh
should add to zero.
I wondered what would happen if random complex numbers
were used for a, b, c, and d,
so I computed the four
mesh
should add to zero.
I wondered what would happen if random complex numbers
were used for a, b, c, and d,
so I computed the four 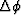 's with equation (76),
and then computed the sum with (78).
They did sum to zero for 2/3 of my random numbers.
Otherwise,
with probability 1/6 each, they summed to
's with equation (76),
and then computed the sum with (78).
They did sum to zero for 2/3 of my random numbers.
Otherwise,
with probability 1/6 each, they summed to 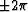 .The nonvanishing curl represents a phase that is changing
too rapidly between the mesh points.
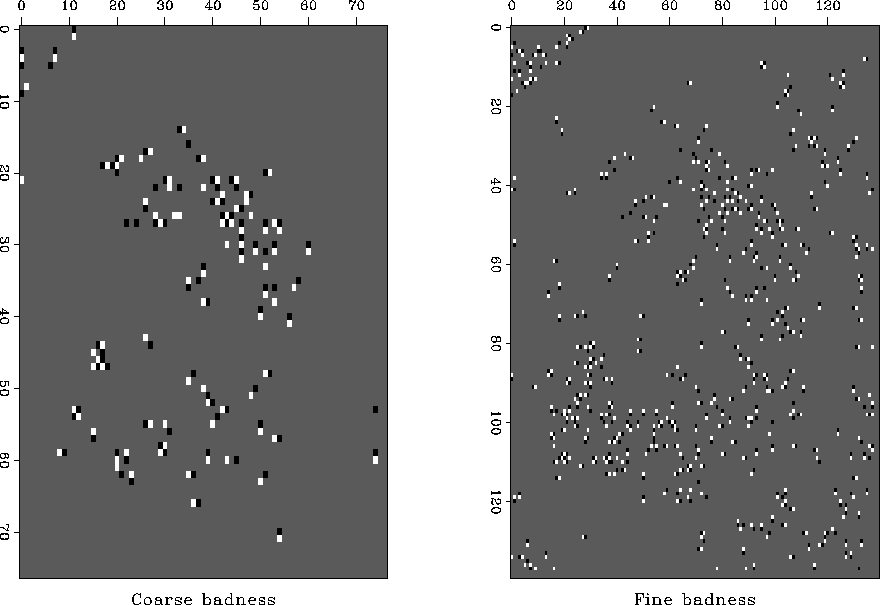
Figure
.The nonvanishing curl represents a phase that is changing
too rapidly between the mesh points.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the locations
at Vesuvius where bad data occurs.
This is shown at two different resolutions.
The figure shows a tendency for
bad points with curl
shows the locations
at Vesuvius where bad data occurs.
This is shown at two different resolutions.
The figure shows a tendency for
bad points with curl 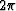 to have a neighbor with
to have a neighbor with 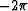 .If Vesuvius were random noise instead of good data,
the planes in Figure
.If Vesuvius were random noise instead of good data,
the planes in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) would be one-third covered with dots
but as expected, we see considerably fewer.
would be one-third covered with dots
but as expected, we see considerably fewer.
screw90
Figure 4
Values of curl at Vesuvius.
The bad data locations at both coarse and fine resolution
tend to occur in pairs of opposite polarity.
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)










Next: Estimating the inverse gradient
Up: VESUVIUS PHASE UNWRAPPING
Previous: VESUVIUS PHASE UNWRAPPING
Stanford Exploration Project
4/27/2004
![\begin{displaymath}
\left[
\begin{array}
{rrrr}
-1 & 1& 0& 0 \\ 0 & 0& -1& 1 ...
... \\ \Delta \phi_{ac} \\ \Delta \phi_{bd}
\end{array}\right]\end{displaymath}](img189.gif)
![\begin{displaymath}
\left[
\begin{array}
{rrrr}
-1 & 1& 0& 0 \\ 0 & 0& -1& 1 ...
... \\ \Delta \phi_{ac} \\ \Delta \phi_{bd}
\end{array}\right]\end{displaymath}](img189.gif)
![]() summed around the
summed around the ![]() mesh
should add to zero.
I wondered what would happen if random complex numbers
were used for a, b, c, and d,
so I computed the four
mesh
should add to zero.
I wondered what would happen if random complex numbers
were used for a, b, c, and d,
so I computed the four ![]() 's with equation (76),
and then computed the sum with (78).
They did sum to zero for 2/3 of my random numbers.
Otherwise,
with probability 1/6 each, they summed to
's with equation (76),
and then computed the sum with (78).
They did sum to zero for 2/3 of my random numbers.
Otherwise,
with probability 1/6 each, they summed to ![]() .The nonvanishing curl represents a phase that is changing
too rapidly between the mesh points.
Figure
.The nonvanishing curl represents a phase that is changing
too rapidly between the mesh points.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the locations
at Vesuvius where bad data occurs.
This is shown at two different resolutions.
The figure shows a tendency for
bad points with curl
shows the locations
at Vesuvius where bad data occurs.
This is shown at two different resolutions.
The figure shows a tendency for
bad points with curl ![]() to have a neighbor with
to have a neighbor with ![]() .If Vesuvius were random noise instead of good data,
the planes in Figure
.If Vesuvius were random noise instead of good data,
the planes in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) would be one-third covered with dots
but as expected, we see considerably fewer.
would be one-third covered with dots
but as expected, we see considerably fewer.