




Next: CAUSALITY AND WAVE PROPAGATION
Up: Spectral factorization
Previous: WHITTLE'S EXP-LOG METHOD
If in a computer we have the coefficients 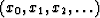 of a
polynomial X(Z),
we say we are ``working in the time domain.''
If we evaluate the polynomial X(Z) at a number of positions
on the unit circle,
we have numbers,
say
of a
polynomial X(Z),
we say we are ``working in the time domain.''
If we evaluate the polynomial X(Z) at a number of positions
on the unit circle,
we have numbers,
say 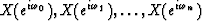 ,which we call a frequency-domain representation of the polynomial X(Z).
We have seen that the fast Fourier transform is a very cheap way of
going from the time domain to the frequency domain and back.
This makes it very worthwhile to look at Whittle's factorization method
in the frequency domain.
Furthermore, we will understand spectral factorization
from yet another point of view.
,which we call a frequency-domain representation of the polynomial X(Z).
We have seen that the fast Fourier transform is a very cheap way of
going from the time domain to the frequency domain and back.
This makes it very worthwhile to look at Whittle's factorization method
in the frequency domain.
Furthermore, we will understand spectral factorization
from yet another point of view.
We may begin with a time function or Z transform
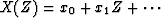 .Let us denote by Xk the transform of the time function,
that is, X(Z) evaluated at numerous
.Let us denote by Xk the transform of the time function,
that is, X(Z) evaluated at numerous 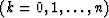 places on the unit circle.
Consider the identities
places on the unit circle.
Consider the identities
Now we add and subtract a still arbitrary function 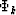 to the
exponential
Now the big question is what
to the
exponential
Now the big question is what 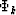 should be used
to guarantee that Bk transforms to a minimum-phase,
one-sided time function?
By looking at Whittle's method,
we note that the only significant properties
of U+ (Z) are that it is finite
and that the time function ut vanishes before t = 0.
Thus we expect that
should be used
to guarantee that Bk transforms to a minimum-phase,
one-sided time function?
By looking at Whittle's method,
we note that the only significant properties
of U+ (Z) are that it is finite
and that the time function ut vanishes before t = 0.
Thus we expect that 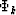 should be chosen
so that when
should be chosen
so that when 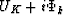 is transformed into the time domain
the resulting time function u+t should vanish for negative time.
This may be done as depicted in Figure 4.
is transformed into the time domain
the resulting time function u+t should vanish for negative time.
This may be done as depicted in Figure 4.
3-4
Figure 4
Determination of the phase function.
|
| 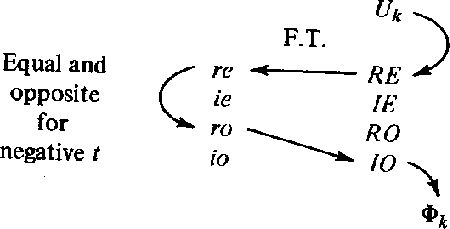 |

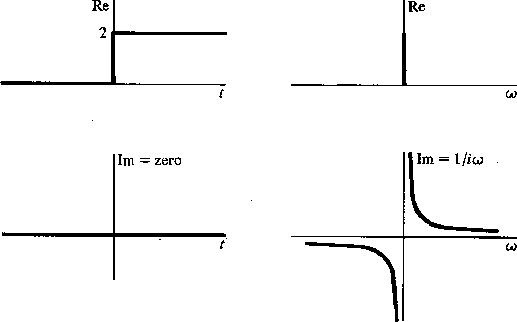
To see how easy it really is to get the imaginary odd part IO,
we fetch the integration filter
from Sec. 2-8 (on bilinear transformation) and
display it in Figure 5.
3-5
Figure 5
The transform pair used in the Hilbert transform.

To get 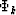 we take Uk into the time domain,
getting ut.
Then we multiply by the real step function of time in Figure 5,
obtaining
we take Uk into the time domain,
getting ut.
Then we multiply by the real step function of time in Figure 5,
obtaining 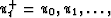 .This implies that in the frequency domain Uk has been convolved
with
.This implies that in the frequency domain Uk has been convolved
with 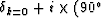 phase shift filter).
Thus,
phase shift filter).
Thus, 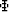 has been generated.
has been generated.
Let us reconsider the operation of dropping all of the negative powers of
Z in U(Z) as we did in the previous section to get U+ (Z).
For simplicity, consider the case rt real; then ut is real.
Now let us make up a new function 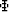 by replacing cosine by sine in
the foregoing expression
by replacing cosine by sine in
the foregoing expression
We now see that combining U with 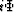 we get U+.
Notice that the operation of changing cos t to sin t would be called
90
we get U+.
Notice that the operation of changing cos t to sin t would be called
90 phase shift filtering.
Here we have changed cos
phase shift filtering.
Here we have changed cos 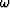 to sin
to sin 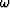 with the result
that U+ (Z) has only positive coefficients of Z.
with the result
that U+ (Z) has only positive coefficients of Z.
The Kolmogoroff method of spectral factorization is very fast in a computer
because fast Fourier transforms may be used.
Its principle disadvantage is
that summation around the unit circle is always slightly different than
integration about the circle.
When the spectrum is simple but poles are very
close to the unit circle,
then the Toeplitz method may prove more satisfactory.
A simple program to do spectral factorization is given in Figure 6.
EXERCISES:
- Insert the additional arrows in Figure 4 which are required when
dealing with complex time functions.
- What is the meaning of minimum-phase waveform if the roles of time
domain and frequency domain are interchanged?
- Show how to do the inverse Hilbert transform, given
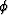 find u.
What is the interpretation of the fact that you cannot get u0?
find u.
What is the interpretation of the fact that you cannot get u0?
- Consider a model of a portion of the earth where x is the north
coordinate, +z represents altitude above the earth,
and magnetic bodies are distributed in the earth so as to create
no magnetic field component in the east-west direction.
One may show that the magnetic field h above the earth is represented by
![\begin{displaymath}
\left[
\begin{array}
{cc}
h_x (x, z) \\ h_z (x, z) \end{arr...
...t k\vert \end{array} \right] \,
e^{ikx - \vert k\vert z} \, dk \end{displaymath}](img90.gif)
Here F(k) is some spatial frequency spectrum.
- (a)
- By using Fourier transforms,
how does one compute hx(x, 0) from
hz (x, 0) and vice versa?
- (b)
- Given hz(x, 0), how does one compute hz(x, z)?
- (c)
- Notice that at z = 0
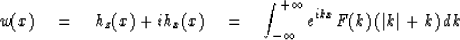
-
- and that F(k) (|k| + k) is a one-sided function of k.
With a total field magnetometer one observes

What can you say about getting F(k) from this?
- (d)
- How unique are hx(x) and hz(x) if
 is given?
is given?
3-6
Figure 6
A program to do spectral factorization by means
of fast Fourier transform and Hilbert transform.
Complex arithmetic is mandatory.
Results are approximate since integration around the unit circle has
been approximated by summation over four points.






Next: CAUSALITY AND WAVE PROPAGATION
Up: Spectral factorization
Previous: WHITTLE'S EXP-LOG METHOD
Stanford Exploration Project
10/30/1997
![]() .Let us denote by Xk the transform of the time function,
that is, X(Z) evaluated at numerous
.Let us denote by Xk the transform of the time function,
that is, X(Z) evaluated at numerous ![]() places on the unit circle.
Consider the identities
places on the unit circle.
Consider the identities
![\begin{eqnarraystar}
R_k &= & \exp \left[ {1 \over 2} (U_k - i\Phi_k) \right] \,...
...eft[ {1 \over 2} (U_k + i\Phi_k) \right] \\ &= & \bar B_k B_k\end{eqnarraystar}](img78.gif)

![]() we take Uk into the time domain,
getting ut.
Then we multiply by the real step function of time in Figure 5,
obtaining
we take Uk into the time domain,
getting ut.
Then we multiply by the real step function of time in Figure 5,
obtaining ![]() .This implies that in the frequency domain Uk has been convolved
with
.This implies that in the frequency domain Uk has been convolved
with ![]() phase shift filter).
Thus,
phase shift filter).
Thus, ![]() has been generated.
has been generated.
![]()
![]()
![]()
![]()
