




Next: THE KOLMOGOROFF METHOD
Up: Spectral factorization
Previous: THE TOEPLITZ METHOD
In this method of spectral factorization
we substitute power series into other power series.
Thus, like the root method, it is good for learning but not good
for computing.
We start with some given autocorrelation rt where
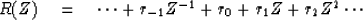
If |R|>2 on the unit circle
then a scale factor should be divided out.
Insert this power series
into the power series for logarithms.
Of course,
in practice this would be a lot of effort,
but it could be done in a systematic fashion with a computer program.
Now define U+t by dropping negative powers of Z from U(Z)
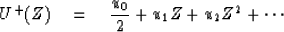
Insert this into the power series for the exponential
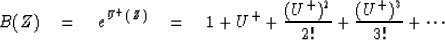
The desired minimum-phase wavelet is B(Z);
its spectrum is R(Z).
To see why this is so,
consider the following identities.
Thus we have factored R(Z) into the desired conjugate parts.
Finally, let us see why B(Z) = eU+ (Z) is minimum phase.
All we need to know about U+(Z) is that it is finite
and does not contain powers of Z-1.
There are two proofs.
The first proof goes by observing that the imaginary part of U(Z) on the
unit circle is the phase angle of B(Z).
To be minimum phase, the phase of B(Z) must not be augmented
by multiples of 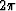 as Z goes around the unit circle.
For minimum phase, the phase should be periodic with period
as Z goes around the unit circle.
For minimum phase, the phase should be periodic with period 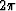 .The phase
.The phase 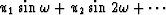 obviously
satisfies this condition.
The second proof is more abstract.
In the second proof we note that the only way
for B(Z0) = eU+ (Z0) to be zero
for some Z0 would be if U+ (Z0) were equal to
obviously
satisfies this condition.
The second proof is more abstract.
In the second proof we note that the only way
for B(Z0) = eU+ (Z0) to be zero
for some Z0 would be if U+ (Z0) were equal to 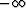 ;in other words, if U+ were nonconvergent.
This is impossible inside the unit circle
because we took the log series for U(Z) to be absolutely convergent
on the unit circle;
this means U+(Z) is convergent (finite) inside the circle.
Since B(Z) cannot have zeros inside the unit circle,
it must be minimum phase.
;in other words, if U+ were nonconvergent.
This is impossible inside the unit circle
because we took the log series for U(Z) to be absolutely convergent
on the unit circle;
this means U+(Z) is convergent (finite) inside the circle.
Since B(Z) cannot have zeros inside the unit circle,
it must be minimum phase.
EXERCISES:
- How can you get B(Z) if |R| > 2 on the unit circle?
- Suppose U+ (Z) = aZ. For values of a = -1, 0, 1, 100, and i sketch
the time function associated with B(Z).
Also sketch their spectra.
Find one which resembles a gaussian.
- Seismograms may be spectrally balanced by dividing the F.T.
of each seismogram by its magnitude and multiplying by the average magnitude.
This amounts to convolution with a symmetrical filter.
How can spectral balancing be defined with causal filters?
- Examine the coefficients of the Z derivative of
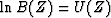 to
find a recurrence for uk given bk and for bk given uk.
to
find a recurrence for uk given bk and for bk given uk.





Next: THE KOLMOGOROFF METHOD
Up: Spectral factorization
Previous: THE TOEPLITZ METHOD
Stanford Exploration Project
10/30/1997
![]()
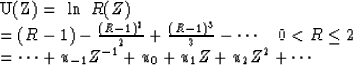
![]()
![]()
![\begin{eqnarraystar}
R(Z) &= & e^{\ln R(Z)} \\ &= & \exp\, \left( {u_0 \over 2} ...
...exp [ U^+ (Z)]\\ &= & B\,
\left( {1 \over Z} \right) \, B(Z)\end{eqnarraystar}](img67.gif)
![]() as Z goes around the unit circle.
For minimum phase, the phase should be periodic with period
as Z goes around the unit circle.
For minimum phase, the phase should be periodic with period ![]() .The phase
.The phase ![]() obviously
satisfies this condition.
The second proof is more abstract.
In the second proof we note that the only way
for B(Z0) = eU+ (Z0) to be zero
for some Z0 would be if U+ (Z0) were equal to
obviously
satisfies this condition.
The second proof is more abstract.
In the second proof we note that the only way
for B(Z0) = eU+ (Z0) to be zero
for some Z0 would be if U+ (Z0) were equal to ![]() ;in other words, if U+ were nonconvergent.
This is impossible inside the unit circle
because we took the log series for U(Z) to be absolutely convergent
on the unit circle;
this means U+(Z) is convergent (finite) inside the circle.
Since B(Z) cannot have zeros inside the unit circle,
it must be minimum phase.
;in other words, if U+ were nonconvergent.
This is impossible inside the unit circle
because we took the log series for U(Z) to be absolutely convergent
on the unit circle;
this means U+(Z) is convergent (finite) inside the circle.
Since B(Z) cannot have zeros inside the unit circle,
it must be minimum phase.