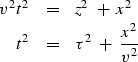CURVED WAVEFRONTS

The simplest waves are expanding circles. An equation for a circle expanding with velocity v is  

$$v^2 \, t^2 \eq x^2 \ \ +\ \ z^2$$ (15)

Considering t to be a constant, i.e. taking a snapshot, equation (15) is that of a circle. Considering z to be a constant, it is an equation in the (x , t)-plane for a hyperbola. Considered in the (t , x , z)-volume, equation (15) is that of a cone. Slices at various values of t show circles of various sizes. Slices of various values of z show various hyperbolas.

Converting equation (15) to traveltime depth $\tau$ we get

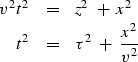$$\begin{eqnarray} v^2 \, t^2 &=& z^2 \ +\ x^2 \\ t^2 &=& \tau^2 \ +\ { x^2 \over v^2 }\end{eqnarray}$$ (16) (17)

The earth's velocity typically increases by more than a factor of two between the earth's surface, and reflectors of interest. Thus we might expect that equation (17) would have little practical use. Luckily, this simple equation will solve many problems for us if we know how to interpret the velocity as an average velocity.