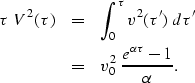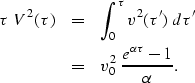Next: About this document ...
Up: CURVED WAVEFRONTS
Previous: Velocity increasing linearly with
Substituting the theoretical interval velocity 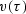 from equation (40)
into the definition of
RMS velocity
from equation (40)
into the definition of
RMS velocity 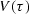 (equation (25))
yields:
(equation (25))
yields:
| 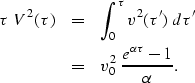 |
(47) |
| (48) |
Thus the desired expression for RMS velocity
as a function of traveltime depth is:
| 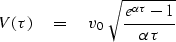 |
(49) |
For small values of 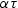 ,this can be approximated as
,this can be approximated as
| 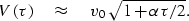 |
(50) |





Next: About this document ...
Up: CURVED WAVEFRONTS
Previous: Velocity increasing linearly with
Stanford Exploration Project
12/26/2000