




Next: The leapfrog method
Up: FINITE DIFFERENCING IN (omega,x)-SPACE
Previous: First derivatives, implicit method
The heat-flow equation (6)
is a prototype for migration. Let us recopy
the heatflow equation letting q denote the temperature.
| 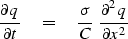 |
(23) |
Implementing (23)
in a computer requires some difference approximations
for the partial differentials.
As before we use a subscript notation
that allows (20) to be compacted into
| 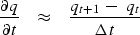 |
(24) |
where 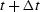 is denoted by t+1.
The second-derivative formula may be obtained by doing the first
derivative twice.
This leads to
is denoted by t+1.
The second-derivative formula may be obtained by doing the first
derivative twice.
This leads to 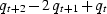 .The formula is usually treated more symmetrically by shifting
it to
.The formula is usually treated more symmetrically by shifting
it to 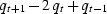 .These two versions
are equivalent as
.These two versions
are equivalent as 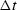 tends to zero, but the more symmetrical
arrangement will be more accurate when
tends to zero, but the more symmetrical
arrangement will be more accurate when 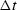 is not zero.
Using superscripts to describe x-dependence gives a finite-difference
approximation to the second space derivative:
is not zero.
Using superscripts to describe x-dependence gives a finite-difference
approximation to the second space derivative:
| 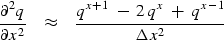 |
(25) |
Inserting the last two equations into the heat-flow equation
(and using = to denote 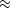 ) gives
) gives
Table 1:
Differencing star and table
for one-dimensional heat-flow equation.
|
|
| 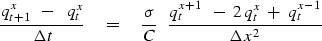 |
(26) |
(Of course it is not justified to use
= to denote 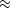 ,but the study of errors must be deferred until the concepts
have been laid out.
Errors are studied in IEI chapter 4.
Letting
,but the study of errors must be deferred until the concepts
have been laid out.
Errors are studied in IEI chapter 4.
Letting 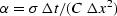 ,equation (26) becomes
,equation (26) becomes
| 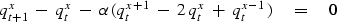 |
(27) |
Equation (27) can be explicitly solved for
q for any x at the particular time t+1
given q at all x for the particular time t
and hence the name explicit method.
Equation (27) can be interpreted geometrically
as a computational
star in the (x,t)-plane, as depicted in Table ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .1.
By moving the star around in the data table
you will note that it
can be positioned so that only one number at a time (the 1)
lies over an unknown element in the data table.
This enables the computation of subsequent rows
beginning from the top.
By doing this you are solving
the partial-differential equation by the
finite-difference method.
There are many possible arrangements
of initial and side conditions,
such as zero-value side conditions.
Next is a computer program for the job and its result.
.1.
By moving the star around in the data table
you will note that it
can be positioned so that only one number at a time (the 1)
lies over an unknown element in the data table.
This enables the computation of subsequent rows
beginning from the top.
By doing this you are solving
the partial-differential equation by the
finite-difference method.
There are many possible arrangements
of initial and side conditions,
such as zero-value side conditions.
Next is a computer program for the job and its result.





Next: The leapfrog method
Up: FINITE DIFFERENCING IN (omega,x)-SPACE
Previous: First derivatives, implicit method
Stanford Exploration Project
12/26/2000
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .1.
By moving the star around in the data table
you will note that it
can be positioned so that only one number at a time (the 1)
lies over an unknown element in the data table.
This enables the computation of subsequent rows
beginning from the top.
By doing this you are solving
the partial-differential equation by the
finite-difference method.
There are many possible arrangements
of initial and side conditions,
such as zero-value side conditions.
Next is a computer program for the job and its result.
.1.
By moving the star around in the data table
you will note that it
can be positioned so that only one number at a time (the 1)
lies over an unknown element in the data table.
This enables the computation of subsequent rows
beginning from the top.
By doing this you are solving
the partial-differential equation by the
finite-difference method.
There are many possible arrangements
of initial and side conditions,
such as zero-value side conditions.
Next is a computer program for the job and its result.