




Next: Splitting
Up: SPLITTING AND SEPARATION
Previous: SPLITTING AND SEPARATION
We wish to solve equation (5)
by a method involving splitting.
Since equation (5)
is an unfamiliar one,
we turn to the heat-flow equation
which besides being familiar, has no complex numbers.
A two-sentence derivation of the heat-flow equation follows.
(1) The heat
flow Hx in the x-direction equals the
negative of the gradient 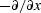 of
temperature T times the heat conductivity
of
temperature T times the heat conductivity  .(2) The decrease of temperature
.(2) The decrease of temperature 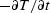 is
proportional to the divergence
of the heat flow
is
proportional to the divergence
of the heat flow 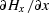 divided by
the heat storage capacity C of the
material.
Combining these, extending from one
dimension to two, taking
divided by
the heat storage capacity C of the
material.
Combining these, extending from one
dimension to two, taking  constant and
constant and 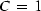 ,gives the equation
,gives the equation
| 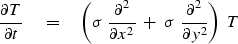 |
(6) |





Next: Splitting
Up: SPLITTING AND SEPARATION
Previous: SPLITTING AND SEPARATION
Stanford Exploration Project
12/26/2000