Damped square root

The definition of k_z as $k_z=\sqrt{\omega^2/v^2 - k_x^2}$obscures two aspects of k_z. First, which of the two square roots is intended, and second, what happens when $k_x^2 \gt \omega^2/v^2$.For both coding and theoretical work we need a definition of ik_z that is valid for both positive and negative values of $\omega$and for all k_x. Define a function $R=ik_z(\omega,k_z)$ by

$$R \quad =\quad ik_z \quad =\quad \sqrt{(-i \omega + \epsilon)^2+k_x^2}$$ (17)

It is important to know that for any $\epsilon \gt$,and any real $\omega$ and real k_x that the real part $\Re R\gt$ is positive. This means we can extrapolate waves safely with e^-Rz for increasing z or with e^+Rz for decreasing z. To switch from downgoing to upcoming we use the complex conjugate $\overline{R}$.Thus we have disentangled the damping from the direction of propagation.

Let us see why $\Re R\gt$ is positive for all real values of $\omega$ and k_x. Recall that for $\omega$ ranging between $\pm\infty$,$e^{i\omega \Delta t}$ rotates around the unit circle in the complex plane. Examine Figure 10 which shows the complex functions:

1.

$f(\omega)= \epsilon - i\omega$,

2.

$-i\hat\omega = (1+\epsilon) -e^{i\omega\Delta t}$,

3.

$(-i \hat\omega)^2$,

4.

$(ik_z)^2 =(-i \hat\omega)^2+k_x^2$, and

5.

$ik_z = [(-i \hat\omega)^2+k_x^2]^{1/2}$

 

francis
Figure 10 Some functions in the complex plane.

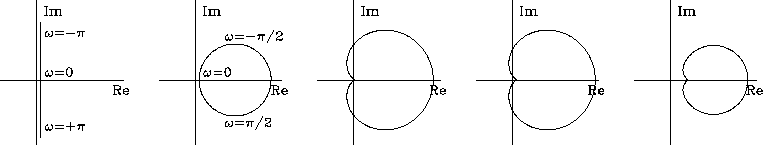The first two panels are explained by the first two functions. The first two functions and the first two panels look different but they become the same in the practical limit of $\epsilon\rightarrow 0$ and $\Delta t \rightarrow 0$.The left panel represents a time derivative in continuous time, and the second panel likewise in sampled time is for a ``causal finite-difference operator'' representing a time derivative. Notice that the graphs look the same near $\omega =0$.As we sample seismic data with increasing density, $\Delta t \rightarrow 0$,the frequency content shifts further away from the Nyquist frequency. Measuring $\omega$ in radians/sample, in the limit $\Delta t \rightarrow 0$, the physical energy is all near $\omega =0$.

The third panel in Figure 10 shows $(-i \hat\omega)^2$ which is a cardioid that wraps itself close up to the negative imaginary axis without touching it. (To understand the shape near the origin, think about the square of the leftmost plane. You may have seen examples of the negative imaginary axis being a branch cut.) In the fourth panel a small positive quantity k_x² is added which shifts the cardioid to the right a bit. Taking the square root gives the last panel which shows the curve in the right half plane thus proving the important result we need, that $\Re\; ik_z(\omega,k_z)\gt$ for all real $\omega$.It is also positive for all real k_x because any k_x²>0 shifts the cardioid to the right. The additional issue of time causality in forward modeling is covered in IEI.

Luckily the Fortran csqrt() function assumes the phase of the argument is between $\pm 180^\circ$exactly as we need here. Thus the square root itself will have a phase between $\pm 90^\circ$as we require. In applications, $\epsilon$would typically be chosen proportional to the maximum time on the data. Thus the mathematical expression $-i\omega + \epsilon$might be rendered in Fortran as cmplx(qi,-omega) where qi=1./tmax and the whole concept implemented as in function eiktau() . Do not set qi=0 because then the csqrt() function cannot decipher positive from negative frequencies.

 

complex function eiktau( dt, w, vkx, qi )
real                     dt, w, vkx, qi
eiktau = cexp( - dt * csqrt( cmplx( qi, -w) ** 2   +   vkx * vkx /4. ) )
return; end

Finally, you might ask, why bother with all this careful theory connected with the damped square root. Why not simply abandon the evanescent waves as done by the ``if'' statement in subroutines phasemig() and phasemod()? There are several reasons:

1.

The exploding reflector concept fails for evanescent waves (when $\omega^2 < v^2k_x^2$). Realistic modeling would have them damping with depth. Rather than trying to handle them correctly we will make a choice, either (1) to abandon evanescent waves effectively setting them to zero, or (2) we will take them to be damping. (You might notice that when we switch from downgoing to upgoing, a damping exponential switches to a growing exponential, but when we consider the adjoint of applying a damped exponential, that adjoint is also a damped exponential.)

I'm not sure if there is a practical difference between choosing to damp evanescent waves or simply to set them to zero, but there should be a noticable difference on synthetic data: When a Fourier-domain amplitude drops abruptly from unity to zero, we can expect a time-domain signal that spreads widely on the time axis, perhaps dropping off slowly as 1/t. We can expect a more concentrated pulse if we include the evanescent energy, even though it is small. I predict the following behavior: Take an impulse; diffract it and then migrate it. When evanescent waves have been truncated, I predict the impulse is turned into a ``butterfly'' whose wings are at the hyperbola asymptote. Damping the evanescent waves, I predict, gives us more of a ``rounded'' impulse.

2.

In a later chapter we will handle the x-axis by finite differencing (so that we can handle v(x). There a stability problem will develop unless we begin from careful definitions as we are doing here.

3.

Seismic theory includes an abstract mathematical concept known as branch-line integrals. Such theory is most easily understood beginning from here.