




Next: Vertical exaggeration example
Up: PHASE-SHIFT MIGRATION
Previous: Damped square root
It is straightforward to adapt the simple programs
phasemig() ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
phasemod()
and
phasemod() ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) to depth variable velocity.
As you might suspect, the two processes are adjoint to each other,
and for reasons given at the end of chapter
to depth variable velocity.
As you might suspect, the two processes are adjoint to each other,
and for reasons given at the end of chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) it is desirable to code them to be so.
With differential equations and their boundary conditions,
the concept of adjoint is more subtle than previous examples.
Thus, I postponed till here the development of adjoint code
for phase-shift migration.
This coding is a little strenuous,
but it affords a review of many basic concepts,
so we do so here. (Feel free to skip this section.)
It is nice to have a high quality code for this fundamental operation.
it is desirable to code them to be so.
With differential equations and their boundary conditions,
the concept of adjoint is more subtle than previous examples.
Thus, I postponed till here the development of adjoint code
for phase-shift migration.
This coding is a little strenuous,
but it affords a review of many basic concepts,
so we do so here. (Feel free to skip this section.)
It is nice to have a high quality code for this fundamental operation.
Many situations in physics are expressed by the differential equation
| 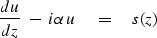 |
(18) |
In the migration application,
u(z) is the up-coming wave,
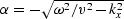 ,s(z) is the exploding-reflector source.
We take the medium to be layered
(v constant in layers)
so that
,s(z) is the exploding-reflector source.
We take the medium to be layered
(v constant in layers)
so that  is constant in a layer,
and we put the sources at the layer boundaries.
Thus within a layer we have
is constant in a layer,
and we put the sources at the layer boundaries.
Thus within a layer we have 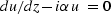 which has the solution
which has the solution
| 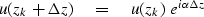 |
(19) |
For convenience, we use the ``delay operator''
in the k-th layer
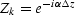 so the delay of upward propagation is expressed by
so the delay of upward propagation is expressed by
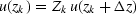 .(Since
.(Since  is negative for upcoming waves,
is negative for upcoming waves,
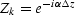 has a positive exponent which represents delay.)
Besides crossing layers, we must cross layer boundaries
where the (reflection) sources add to the upcoming wave.
Thus we have
has a positive exponent which represents delay.)
Besides crossing layers, we must cross layer boundaries
where the (reflection) sources add to the upcoming wave.
Thus we have
| 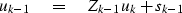 |
(20) |
Recursive use of equation (20) across a medium
of three layers is expressed in matrix form as
| ![\begin{displaymath}
\bold M \, \bold u \quad =\quad
\left[
\begin{array}
{cccc}...
...\ s_1 \\ s_2 \\ s_3
\end{array} \right]
\quad =\quad\bold s\end{displaymath}](img79.gif) |
(21) |
A recursive solution begins at the bottom
with u3=s3 and propagates upward.
The adjoint (complex conjugate) of the delay operator Z
is the time advance operator 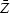 .The adjoint of equation (21)
is given by
.The adjoint of equation (21)
is given by
| ![\begin{displaymath}
\bold M' \, \tilde {\bold s} \quad =\quad
\left[
\begin{arr...
...u_1 \\ u_2 \\ u_3
\end{array} \right] \
\quad =\quad\bold u\end{displaymath}](img81.gif) |
(22) |
where 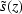 (summed over frequency) is the migrated image.
The adjointness of equation (21) and (22)
seems obvious,
but it is not the elementary form we are familiar with
because the matrix multiplies the output
(instead of multiplying the usual input).
To prove the adjointness, notice that
equation (21)
is equivalent to
(summed over frequency) is the migrated image.
The adjointness of equation (21) and (22)
seems obvious,
but it is not the elementary form we are familiar with
because the matrix multiplies the output
(instead of multiplying the usual input).
To prove the adjointness, notice that
equation (21)
is equivalent to 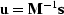 whose
adjoint, by definition,
is
whose
adjoint, by definition,
is 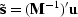 which
is
which
is 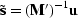 (because of the basic mathematical fact
that the adjoint of an inverse is the inverse of the adjoint)
which gives
(because of the basic mathematical fact
that the adjoint of an inverse is the inverse of the adjoint)
which gives 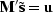 which is equation (22).
which is equation (22).
We observe the wavefield only on the surface z=0,
so the adjointness of
equations (21)
and (22)
is academic because it relates the wavefield at all depths
with the source at all depths.
We need to truncate  to its first coefficient u0
since the upcoming wave is known only at the surface.
This truncation changes the adjoint in a curious way.
We rewrite equation (21)
using a truncation operator
to its first coefficient u0
since the upcoming wave is known only at the surface.
This truncation changes the adjoint in a curious way.
We rewrite equation (21)
using a truncation operator 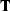 that is
the row matrix
that is
the row matrix ![$\bold T = [1,0,0,\cdots ]$](img89.gif) getting
getting
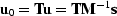 .Its adjoint is
.Its adjoint is
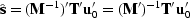 or
or
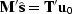 which looks like
which looks like
| ![\begin{displaymath}
\bold M' \, \tilde {\bold s} \quad =\quad
\left[
\begin{arr...
...begin{array}
{c}
u_0 \\ 0 \\ 0 \\ 0
\end{array} \right] \\ end{displaymath}](img93.gif) |
(23) |
The operator 23 is a recursion
beginning from 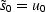 and continuing downward with
and continuing downward with
| 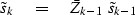 |
(24) |
A final feature of the migration application
is that the image is formed from 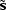 by summing over all frequencies.
Although I believe the mathematics above
and the code in subroutine gazadj()
by summing over all frequencies.
Although I believe the mathematics above
and the code in subroutine gazadj() ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
I ran the dot product test to be sure!
,
I ran the dot product test to be sure!
# Phase shift modeling and migration. (Warning: destroys its input!)
#
subroutine gazadj( adj, dt,dx, v,nt,nx, modl, data )
integer adj, nt,nx, iw, ikx, iz,nz
complex eiktau, cup, modl(nt,nx), data(nt,nx)
real dt,dx, v(nt), pi, w,w0,dw, kx,kx0,dkx,qi
call adjnull( adj, 0, modl,nt*nx*2, data,nt*nx*2 )
pi = 4.*atan(1.); w0 = -pi/dt; dw = 2.*pi/(nt*dt); qi=.5/(nt*dt)
nz = nt; kx0 = -pi/dx; dkx= 2.*pi/(nx*dx)
if( adj == 0) call ft2axis( 0, -1., nz, nx, modl)
else { call ft2axis( 0, -1., nt, nx, data)
call ft1axis( 0, 1., nt, nx, data)
}
do ikx = 2, nx { kx = kx0 + (ikx-1) * dkx
do iw = 2, 1+nt/2 { w = w0 + (iw -1) * dw
if( adj== 0) { data(iw,ikx) = modl(nz,ikx)
do iz = nz-1, 1, -1
data(iw,ikx) = data(iw,ikx) * eiktau(dt,w,v(iz)*kx,qi) +
modl(iz,ikx)
}
else { cup = data(iw,ikx)
do iz = 1, nz {
modl(iz,ikx) = modl(iz,ikx) + cup
cup = cup * conjg( eiktau(dt,w,v(iz)*kx,qi))
}
}
}}
if( adj == 0) { call ft1axis( 1, 1., nt, nx, data)
call ft2axis( 1, -1., nt, nx, data) }
else { call ft2axis( 1, -1., nz, nx, modl) }
return; end
Finally, a few small details about the code.
The loop on spatial frequency ikx
begins at ikx=2.
The reason for the 2, instead of a 1,
is to omit the Nyquist frequency.
If the Nyquist frequency were to be included,
it should be divided into one half at positive Nyquist and one half
at negative Nyquist, which would clutter the code
without adding practical value.
Another small detail is that the loop
on temporal frequency iw
begins at iw=1+nt/2
which effectly omits negative frequencies.
This is purely an economy measure.
Including the negative frequencies would assure that the
final image be real, no imaginary part.
Omitting negative frequencies simply gives an imaginary part
that can be thrown away,
and gives the same real image, scaled by a half.
The factor of two speed up makes these tiny compromises well worthwhile.





Next: Vertical exaggeration example
Up: PHASE-SHIFT MIGRATION
Previous: Damped square root
Stanford Exploration Project
12/26/2000
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
phasemod()
and
phasemod() ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) to depth variable velocity.
As you might suspect, the two processes are adjoint to each other,
and for reasons given at the end of chapter
to depth variable velocity.
As you might suspect, the two processes are adjoint to each other,
and for reasons given at the end of chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) it is desirable to code them to be so.
With differential equations and their boundary conditions,
the concept of adjoint is more subtle than previous examples.
Thus, I postponed till here the development of adjoint code
for phase-shift migration.
This coding is a little strenuous,
but it affords a review of many basic concepts,
so we do so here. (Feel free to skip this section.)
It is nice to have a high quality code for this fundamental operation.
it is desirable to code them to be so.
With differential equations and their boundary conditions,
the concept of adjoint is more subtle than previous examples.
Thus, I postponed till here the development of adjoint code
for phase-shift migration.
This coding is a little strenuous,
but it affords a review of many basic concepts,
so we do so here. (Feel free to skip this section.)
It is nice to have a high quality code for this fundamental operation.
![\begin{displaymath}
\bold M \, \bold u \quad =\quad
\left[
\begin{array}
{cccc}...
...\ s_1 \\ s_2 \\ s_3
\end{array} \right]
\quad =\quad\bold s\end{displaymath}](img79.gif)
![\begin{displaymath}
\bold M' \, \tilde {\bold s} \quad =\quad
\left[
\begin{arr...
...u_1 \\ u_2 \\ u_3
\end{array} \right] \
\quad =\quad\bold u\end{displaymath}](img81.gif)
![\begin{displaymath}
\bold M' \, \tilde {\bold s} \quad =\quad
\left[
\begin{arr...
...begin{array}
{c}
u_0 \\ 0 \\ 0 \\ 0
\end{array} \right] \\ end{displaymath}](img93.gif)