A FULLY TWO-DIMENSIONAL PE FILTER

 The prediction-error filters we dealt with above are not genuinely two-dimensional because Fourier transform over time would leave independent, 1-D, spatial PE filters for each temporal frequency.

What is a truly

two-dimensional prediction-error filter? This is a question we should answer in our quest to understand resonant signals aligned along various dips. Figure 11 shows that an interpolation-error filter is no substitute for a PE filter in one dimension. So we need to use special care in properly defining a 2-D PE filter. Recall the basic proof in chapter (page ) that the output of a PE filter is white. The basic idea is that the output residual is uncorrelated with the input fitting functions (delayed signals); hence, by linear combination, the output is uncorrelated with the past outputs (because past outputs are also linear combinations of past inputs). This is proven for one side of the autocorrelation, and the last step in the proof is to note that what is true for one side of the autocorrelation must be true for the other. Therefore, we need to extend the idea of ``past'' and ``future'' into the plane to divide the plane into two halves. Thus I generally take a 2-D PE filter to be of the form

$$\begin{array} {ccccccc} a &a &a &a &a &a &a \ a &a &a &a ... ...\ \cdot &\cdot &\cdot &\cdot &\cdot &\cdot &\cdot \end{array}$$ (12)

where ``$\cdot$'' marks the location of a zero element and a marks the location of an element that is found by minimizing the output power. Notice that for each a, there is a point mirrored across the ``1'' at the origin, and the mirrored point is not in the filter. Together, all the a locations and their mirrors cover the plane. Obviously the plane can be bisected in other ways, but this way seems a natural one for the processes we have in mind.

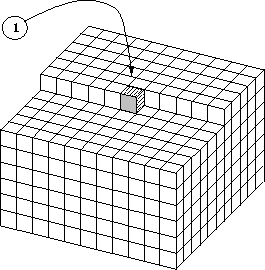
The three-dimensional prediction-error filter

which embodies the same concept is shown in Figure 21.

 

3dpef Figure 21 Three-dimensional prediction-error filter.

Can ``short'' filters be used? Experience shows that a significant detriment to whitening with a PE filter is an underlying model that is not purely a polynomial division because it has a convolutional (moving average) part. The convolutional part is especially troublesome when it involves serious bandlimiting, as does convolution with bionomial coefficients (for example, the Butterworth filter, discussed in chapter ). When bandlimiting occurs, it seems best to use a gapped PE filter.

I have some limited experience with 2-D PE filters that suggests using a gapped form like

$$\begin{array} {ccccccccc} a &a &a &a &a &a &a &a &a \ a &... ...a \ \cdot &\cdot &\cdot &1 &\cdot &\cdot &a &a &a \end{array}$$ (13)

With this kind of PE filter, the output traces are uncorrelated with each other, and the output plane is correlated with itself only for a short distance (the length of the gap) on the time axis.

EXERCISES:

1. Recall Figure . Explain how to do the job properly.