Limitations of the exploding-reflector concept

The exploding-reflector concept is a powerful and fortunate analogy. For people who spend their time working entirely on data interpretation rather than on processing, the exploding-reflector concept is more than a vital crutch. It's the only means of transportation! But for those of us who work on data processing, the exploding-reflector concept has a serious shortcoming. No one has yet figured out how to extend the concept to apply to data recorded at nonzero offset. Furthermore, most data is recorded at rather large offsets. In a modern marine prospecting survey, there is not one hydrophone, but hundreds, which are strung out in a cable towed behind the ship. The recording cable is typically 2-3 kilometers long. Drilling may be about 3 kilometers deep. So in practice the angles are big. Therein lie both new problems and new opportunities, none of which will be considered until chapter .

Furthermore, even at zero offset, the exploding-reflector concept is not quantitatively correct. For the moment, note three obvious failings: First, Figure 8 shows rays that are not predicted by the exploding-reflector model.

 

fail
Figure 8 Two rays, not predicted by the exploding-reflector model, that would nevertheless be found on a zero-offset section.

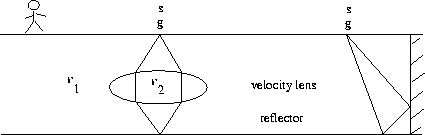These rays will be present in a zero-offset section. Lateral velocity variation is required for this situation to exist.

Second, the exploding-reflector concept fails with multiple reflections. For a flat sea floor with a two-way travel time t₁, multiple reflections are predicted at times 2t₁, 3t₁, 4t₁, etc. In the exploding-reflector geometry the first multiple goes from reflector to surface, then from surface to reflector, then from reflector to surface, for a total time 3t₁. Subsequent multiples occur at times 5t₁, 7t₁, etc. Clearly the multiple reflections generated on the zero-offset section differ from those of the exploding-reflector model.

The third failing of the exploding-reflector model is where we are able to see waves bounced from both sides of an interface. The exploding-reflector model predicts the waves emitted by both sides have the same polarity. The physics of reflection coefficients says reflections from opposite sides have opposite polarities.