Consider a vertical wall, a limiting case of a dipping bed. Its reflections, the asymptotes of a hyperbola, have a nonvertical steepness. This establishes that migration increases the apparent steepness of dipping beds. I use the words apparent steepness because it is the slope as seen in the (x,t)-plane that has steepened. Migration really produces its output in z, but z/v is often overlain on t to create a migrated time section . When we say a hyperbola migrates to its apex, we are of course thinking of the migrated time section. Let us determine the steepening as a function of angle.
Consider a point ![]()
![]() ,
, ![]() neighboring
the original point (x0 , t0 ).
By equations (4) and (5), this neighbor migrates to
neighboring
the original point (x0 , t0 ).
By equations (4) and (5), this neighbor migrates to
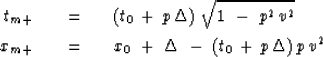 |
(6) | |
| (7) |
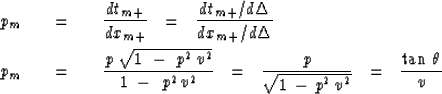 |
||
| (8) |
It may seem paradoxical that dipping beds change slope on migration whereas flanks of hyperbolas do not change slope during downward continuation. One reason is that migration is downward continuation plus imaging (selecting t=0). Another reason is that a hyperbola is a special event that comes from a single source at a single depth whereas a dipping bed is a superposition of point sources from different depths.
 |
Figure 7 shows how points making up a line reflector diffract to a line reflection, and how points making up a line reflection migrate to a line reflector.