




Next: Reflector steepening
Up: EXPLODING REFLECTORS
Previous: An impulse in the
Given a seismic event at ( x0 , t0 ) with a slope 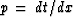 ,let us determine its position ( xm , tm ) after migration.
Consider a planar wavefront at angle
,let us determine its position ( xm , tm ) after migration.
Consider a planar wavefront at angle 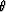 to the earth's surface
traveling a distance dx in a time dt.
Assuming a velocity v we have
the wave angle in terms of measurable quantities.
to the earth's surface
traveling a distance dx in a time dt.
Assuming a velocity v we have
the wave angle in terms of measurable quantities.
| 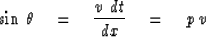 |
(3) |
The vertical travel path is less than the angled path by
| 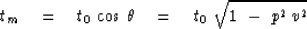 |
(4) |
A travel time t0 and
a horizontal component of velocity 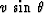 gives
the lateral location after migration:
gives
the lateral location after migration:
| 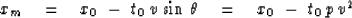 |
(5) |
Consideration of a hyperbola migrating towards its apex shows
why (5) contains a minus sign.
Equations (4) and (5) are the basic equations
for manual migration of reflection seismic data.
They tell you where the point migrates,
but they do not tell you how the slope p will change.





Next: Reflector steepening
Up: EXPLODING REFLECTORS
Previous: An impulse in the
Stanford Exploration Project
10/31/1997
![]() ,let us determine its position ( xm , tm ) after migration.
Consider a planar wavefront at angle
,let us determine its position ( xm , tm ) after migration.
Consider a planar wavefront at angle ![]() to the earth's surface
traveling a distance dx in a time dt.
Assuming a velocity v we have
the wave angle in terms of measurable quantities.
to the earth's surface
traveling a distance dx in a time dt.
Assuming a velocity v we have
the wave angle in terms of measurable quantities.