Linearity allows postponing statistical estimation

The linearity of wave-equation data processing allows us to decompose a dataset into parts, process the parts separately, then recombine them. The result is the same as if they were never separated.

For example, suppose a CMP gather is divided into two parts, say, inner traces A and outer traces B. Let (A,0) denote a CMP gather where the outer traces have been replaced by zeroes. Likewise, (0,B) could be another copy of the gather where the inner traces have been replaced by zeroes. We could downward continue (A,0) and separately downward continue (0,B). After downward continuation, (A,0) and (0,B) could be added. Alternately, we could pause, do some thinking about statistics, and then choose to combine them with some weighting function. 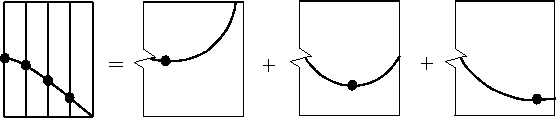Figure 4 shows a dataset of three traces decomposed into three datasets, one for each trace.

 

decomp
Figure 4 A three-trace CMP gather decomposed by traces. At the left, impulses on the data are interpolated, depicting a hyperbola. At the right, data points are expanded into migration semicircles, each of which goes through zero offset at the apex of the hyperbola.

Semicircles depict the separate downward continuation of each trace. Each semicircle goes through zero offset, giving the appropriately stretched, NMOed trace.

The idea of using a weighting function is a drastic departure from our previous style of analysis. It represents a disturbing recognition that we have been neglecting something important in all scientific analysis, namely, statistics! What are the ingredients that go into the choice of a weighting function? They are many. Signal and noise variances play a role. Some channels may be noisy or absent. When final display is contemplated, it is necessary to consider human perception and the need to compress the dynamic range, so that small values can be perceived. Dynamic-range compression must be considered not only in the obvious (h,t)-space, but also in frequency space, dip space, or any other space in which the wavefields may get too far out of balance.

There are many ways to decompose a dataset. The choice depends on your statistical model and your willingness to repeat the processing many times. Perhaps the parts of the data gather should be decomposed not by their h values but by their values of 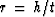$r\,=\,h/t$.Clearly, there is a lot to think about.