The earth's velocity typically ranges over a factor of two or more within the depth range of a given data set. Thus the Pythagorean analysis needs reexamination. In practice, depth variable velocity is often handled by inserting a time variable velocity into the Pythagorean relation. (The classic reference, Taner and Koehler [1969], includes many helpful details). This approximation is much used, although it is not difficult to compute the correct nonhyperbolic moveout. Let us see how the velocity function v(z) is mathematically related to the NMO. Ignoring dip, NMO converts common-midpoint gathers, one of which, say, is denoted by P(h,t), to an earth model, say,
| |
(1) |
The NMO procedure can be regarded as a simple copying. Conceptually, it is easy to think of copying every point of the (h,t)-plane to its appropriate place in the (h,z)-plane. Such a copying process could be denoted as
| |
(2) |
| |
(3) |
Using the terminology of this book, the input P(h,t) to the moveout correction is called a CMP gather, and the output Q is called a CDP gather.
In practice, the first step in generating the travel-time
tables is to change the depth-variable z to
a vertical travel-time-variable ![]() .So the required table is
.So the required table is ![]() ).
To get the output data for location
).
To get the output data for location ![]() ) you take the
input data at location (h,t).
The most straightforward and reliable way to produce this table seems to
be to march down in steps of z, really
) you take the
input data at location (h,t).
The most straightforward and reliable way to produce this table seems to
be to march down in steps of z, really ![]() , and trace rays.
That is, for various fixed values of Snell's parameter p, you
compute
, and trace rays.
That is, for various fixed values of Snell's parameter p, you
compute ![]() and
and ![]() from
from ![]() by integrating
the following equations over
by integrating
the following equations over ![]() :
:
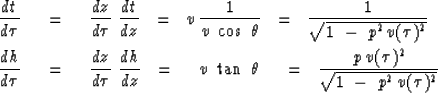 |
(4) | |
| (5) |