The ``true value'' of the mean could be defined by flipping the coin n times and conceiving of n going to infinity. A more convenient definition of ``true value'' is that the experiment could be conceived of as having been done separately under identical conditions by an infinite number of people (an ensemble). Such an artifice will enable us to define a time-variable mean for coins which change with time.
The utility of the concept of an ensemble is often subjected to serious attack both from the point of view of the theoretical foundations of statistics and from the point of view of experimentalists applying the techniques of statistics. Nonetheless a great body of geophysical literature uses the artifice of assuming the existence of an unobservable ensemble. The advocates of using ensembles (the Gibbsians) have the advantage over their adversaries (the Bayesians) in that their mathematics is more tractable (and more explainable). So, let us begin!
A conceptual average over the ensemble, called an expectation, is denoted by the symbol E. The index for summation over the ensemble is never shown explicitly; every random variable is presumed to have one. Thus, the true mean at time t may be defined as
| |
(13) |
| |
(14) |
Likewise, we may be interested in a property of xt called its variance which is a measure of variability about the mean defined by
| |
(15) |
| |
(16) |
| |
(17) |
Now let xt be a time series made up from (identically distributed,
independently chosen)
random numbers in such a way that m and ![]() do not depend on time.
Suppose we have a sample of n points of xt and are
trying to determine the value of m.
We could make an estimate
do not depend on time.
Suppose we have a sample of n points of xt and are
trying to determine the value of m.
We could make an estimate ![]() of the mean m with the formula
of the mean m with the formula
| |
(18) |
| |
(19) |
| |
(20) |
Our objective in this section is to determine how far the estimated mean
![]() is likely to be from the true mean m for a sample of length n.
One possible definition of this excursion
is likely to be from the true mean m for a sample of length n.
One possible definition of this excursion ![]() is
is
![\begin{eqnarray}
(\Delta m)^2 &= & E\, [(\hat{m} - m)^2]
\\ &= & E\, \left\{ [(\sum w_t x_t) - m]^2 \right\}\end{eqnarray}](img49.gif) |
(21) | |
| (22) |
![\begin{eqnarray}
(\Delta m)^2
&= &E\, \left\{ \left[\sum_t w_t (x_t - m) \right...
...\\ &= &E\, \left[\sum_t \sum_s w_t w_s (x_t - m)(x_s - m) \right] \end{eqnarray}](img51.gif) |
(23) | |
| (24) | ||
| (25) |
| |
(26) |
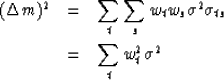 |
(27) | |
| (28) |
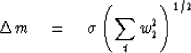 |
(29) |
![\begin{displaymath}
\Delta m \eq \sigma \left[ \sum^n_1 \left( {1 \over n}\right)^2 \right]^{1/2}
\eq {\sigma \over (n)^{1/2}}\end{displaymath}](img55.gif) |
(30) |
When one is trying to estimate the mean of a random series which has a
time-variable mean, one faces a basic dilemma.
If one includes a lot of numbers in the sum to get ![]() small,
then m may be changing while one is trying to measure it.
In contrast,
small,
then m may be changing while one is trying to measure it.
In contrast, ![]() measured from a short sample of the series
might deviate greatly from the true m (defined by an
infinite sum over the ensemble at any point in time).
This is the basic dilemma faced by a stockbroker when a client tells him,
``Since the market fluctuates a lot I'd like you to sell my stock
sometime when the price is above the mean selling price.''
measured from a short sample of the series
might deviate greatly from the true m (defined by an
infinite sum over the ensemble at any point in time).
This is the basic dilemma faced by a stockbroker when a client tells him,
``Since the market fluctuates a lot I'd like you to sell my stock
sometime when the price is above the mean selling price.''
If we imagine that a time series is sampled every ![]() seconds
and we let
seconds
and we let
![]() denote the length of the sample then (30) may be
written as
denote the length of the sample then (30) may be
written as
| |
(31) |
| |
(32) |
In considering other sets of weights one may take a definition of ![]() which is more physically sensible than
which is more physically sensible than ![]() times the number of weights.
For example, if the weights wt are given by a sampled gaussian function as
shown in Figure 2 then
times the number of weights.
For example, if the weights wt are given by a sampled gaussian function as
shown in Figure 2 then ![]() could be taken as the separation of
half-amplitude points,
1/e points, the time span which includes 95 percent of the area,
or it could be given many other ``sensible'' interpretations.
Given a little slop in the definition of
could be taken as the separation of
half-amplitude points,
1/e points, the time span which includes 95 percent of the area,
or it could be given many other ``sensible'' interpretations.
Given a little slop in the definition of ![]() and
and ![]() ,it is clear that the inequality of (32) is not to be strictly applied.
,it is clear that the inequality of (32) is not to be strictly applied.
|
4-1
Figure 2 Binomial coefficients tend to the gaussian function. Plotted are the coefficients of Zt in (.5 + .5Z)20. | 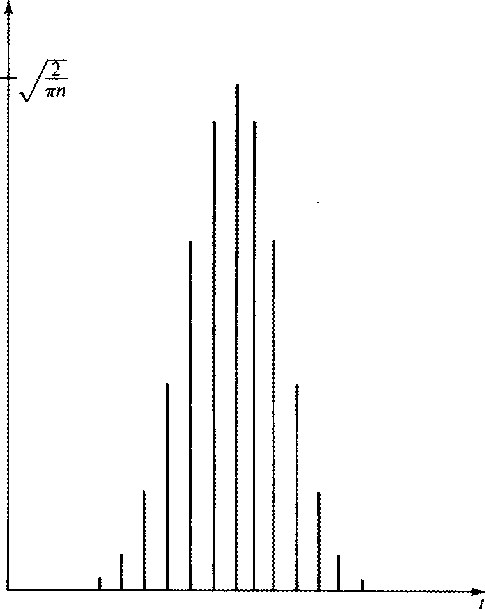 |
Given a sample of a zero mean random time series xt,
we may define another series yt by yt = x2t.
The problem of estimating the variance
![]() of xt is identical to the problem of estimating the mean
m of yt.
If the sample is short,
we may expect an error
of xt is identical to the problem of estimating the mean
m of yt.
If the sample is short,
we may expect an error ![]() in our estimate of the variance.
Thus, in a scientific paper one would like to write for the mean
in our estimate of the variance.
Thus, in a scientific paper one would like to write for the mean
| |
(33) | |
| (34) |
| |
(35) |
Of course (35) really is not right
because we really should add something to indicate additional uncertainty
due to error in ![]() . This estimated error would again have an error, ad infinitum.
To really express the result properly,
it is necessary to have a probability
density function to calculate all the E(xn) which are required.
The probability function can be either estimated from the data
or chosen theoretically.
In practice, for a reason given in a later section,
the gaussian function often occurs.
In the exercise it is shown that
. This estimated error would again have an error, ad infinitum.
To really express the result properly,
it is necessary to have a probability
density function to calculate all the E(xn) which are required.
The probability function can be either estimated from the data
or chosen theoretically.
In practice, for a reason given in a later section,
the gaussian function often occurs.
In the exercise it is shown that
| |
(36) |
| |
(37) |
Correlation is a concept similar to cosine. A cosine measures the angle between two vectors. It is given by the dot product of the two vectors divided by their magnitudes
![]()
![]()
![]()
No doubt this accounts for many false ``discoveries''.
The topic of bias and variance of coherency estimates is a complicated one,
but a rule of thumb seems to be to expect bias and variance
of ![]() on the order of
on the order of ![]() for samples of size n.
for samples of size n.
![]()
![]()
![]()
![]()
![]()