![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)




Next: TIME-FREQUENCY RESOLUTION
Up: Table of Contents
Resolution
In locating an earthquake or a petroleum drilling site there will
be an uncertainty in location,
say 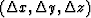 caused
by measurement errors and the physical size of the target.
In measuring a
voltage there will be a measuring accuracy
caused
by measurement errors and the physical size of the target.
In measuring a
voltage there will be a measuring accuracy 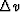 .The frequency of
useful seismic waves will have a bandwidth
.The frequency of
useful seismic waves will have a bandwidth 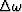 .The time at which
an earthquake occurs will have an uncertainty given by the duration of
shaking
.The time at which
an earthquake occurs will have an uncertainty given by the duration of
shaking 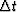 .A telescope of diameter
.A telescope of diameter 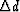 has at best a resolving
power measured by a certain angular range
has at best a resolving
power measured by a certain angular range 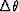 .It is often
desirable to make measurements in such a way as to reduce the quantities
.It is often
desirable to make measurements in such a way as to reduce the quantities
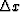 ,
, 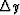 ,
, 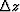 ,
, 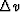 ,
, 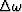 ,
, 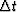 ,
,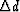 , and
, and 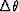 to values as small as possible.
These
measures of resolution (which are called variances, tolerances,
uncertainties, bandwidths, durations, spreads, spans, etc.)
sometimes interact with one another in such a way
that any experimental modification which reduces one
must necessarily increase another or some combination of the others.
The purpose of this chapter is to discuss some of the commonly
occurring situations where such conflicting interactions occur.
to values as small as possible.
These
measures of resolution (which are called variances, tolerances,
uncertainties, bandwidths, durations, spreads, spans, etc.)
sometimes interact with one another in such a way
that any experimental modification which reduces one
must necessarily increase another or some combination of the others.
The purpose of this chapter is to discuss some of the commonly
occurring situations where such conflicting interactions occur.
In this chapter we use 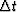 to denote the time duration of a signal.
We use
to denote the time duration of a signal.
We use  to denote the amount of time which passes between sample
points. In other chapters,
to denote the amount of time which passes between sample
points. In other chapters, 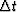 is synonymous with
is synonymous with  , the sample
interval.
, the sample
interval.
![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)




Next: TIME-FREQUENCY RESOLUTION
Up: Table of Contents
Stanford Exploration Project
10/30/1997
![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)
![]() to denote the time duration of a signal.
We use
to denote the time duration of a signal.
We use ![]() to denote the amount of time which passes between sample
points. In other chapters,
to denote the amount of time which passes between sample
points. In other chapters, ![]() is synonymous with
is synonymous with ![]() , the sample
interval.
, the sample
interval.
![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)