![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) at every depth level,
until they meet to image a diffractor at depth.
However, when ray bending occurs, it seems that common-azimuth
downward continuation introduces an error.
This conclusion would be in contradiction
with the accurate results obtained by the application
of common-azimuth migration shown in the next section,
and it requires a closer examination.
We first discuss the simpler case of velocity
varying with depth, and then the general case of velocity
varying laterally.
at every depth level,
until they meet to image a diffractor at depth.
However, when ray bending occurs, it seems that common-azimuth
downward continuation introduces an error.
This conclusion would be in contradiction
with the accurate results obtained by the application
of common-azimuth migration shown in the next section,
and it requires a closer examination.
We first discuss the simpler case of velocity
varying with depth, and then the general case of velocity
varying laterally.
Inspection of the stationary-phase results
[equation (7) and equation (9)]
shows that in a horizontally stratified medium the
cross-line ray parameters for the source and receiver
rays ![]() change across boundaries between layers with different velocities.
This result contradicts
Snell's law that states that the horizontal
ray parameters must be constant when the velocity
varies only vertically.
In common-azimuth downward continuation, by imposing the constraint that the
source and receiver ray must lie on the same plane,
we force the source and receiver rays to bend across interfaces
in a way that may not be consistent with Snell's law.
In particular, the ray bending determined by
common-azimuth continuation is incorrect when
the velocity variations would prescribe
the source ray to bend differently
than the receiver ray along the cross-line direction.
This error in the ray bending can be analyzed by
evaluating the difference between the values of
change across boundaries between layers with different velocities.
This result contradicts
Snell's law that states that the horizontal
ray parameters must be constant when the velocity
varies only vertically.
In common-azimuth downward continuation, by imposing the constraint that the
source and receiver ray must lie on the same plane,
we force the source and receiver rays to bend across interfaces
in a way that may not be consistent with Snell's law.
In particular, the ray bending determined by
common-azimuth continuation is incorrect when
the velocity variations would prescribe
the source ray to bend differently
than the receiver ray along the cross-line direction.
This error in the ray bending can be analyzed by
evaluating the difference between the values of
![]() across an interface where the upper layer has
velocity V1 and the lower layer has velocity V2
across an interface where the upper layer has
velocity V1 and the lower layer has velocity V2
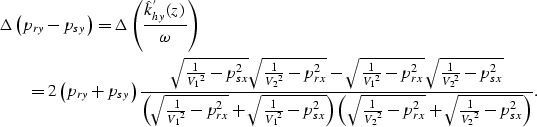 |
||
| (10) |
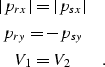 |
(11) | |
| (12) | ||
| (13) |
The previous analysis shows that common-azimuth
downward continuation introduces an error in the ray bending
across velocity interfaces.
However, this consideration does not necessarily
leads to the conclusion that common-azimuth continuation
is inaccurate.
On the contrary, we argue that
the error in the ray bending
causes only second order errors in the continuation results.
This claim can be simply verified by recognizing that
for downward continuing common-azimuth data we evaluate
the phase function ![]() [equation (3)]
at its stationary point
[equation (3)]
at its stationary point ![]() [equation (7)]
with respect to the cross-line offset wavenumber khy.
Since the phase function is stationary at
[equation (7)]
with respect to the cross-line offset wavenumber khy.
Since the phase function is stationary at ![]() the first order term of its Taylor expansion as a
function of khy around
the first order term of its Taylor expansion as a
function of khy around ![]() is equal to zero.
Therefore, an error in khy has only a second order effect
on the evaluation
of the phase function
is equal to zero.
Therefore, an error in khy has only a second order effect
on the evaluation
of the phase function ![]() [equation (6)].
In other words,
the error introduced by the incorrect ray bending
has second order effects on the continuation results,
and consequently on the migration results.
This conclusion is supported by the accuracy
of the migrated images shown in the next section.
[equation (6)].
In other words,
the error introduced by the incorrect ray bending
has second order effects on the continuation results,
and consequently on the migration results.
This conclusion is supported by the accuracy
of the migrated images shown in the next section.
When the velocity field varies laterally, the previous
analysis becomes more complex because the incorrect
ray bending causes errors in the evaluation of
the phase function not only through errors in the cross-line offset
wavenumber ![]() ,but also through errors in the horizontal locations
where the velocity function is evaluated.
The arguments that support the conclusion that
the errors in the phase function caused by error in
,but also through errors in the horizontal locations
where the velocity function is evaluated.
The arguments that support the conclusion that
the errors in the phase function caused by error in ![]() are
of second order are still
valid for the general case of lateral velocity variations.
However, the magnitude of the error introduced by the
mispositioning of sources and receivers at depth when evaluating
the velocity function cannot be neglected in principle.
These errors are dependent on the spatial variability of
the velocity function, and cannot be readily analyzed analytically.
In the following section we show accurate migration results
obtained over a velocity function varying both laterally
and vertically. These results are encouraging and
suggest that the range of application of common-azimuth
migration to depth migration problems is fairly large.
are
of second order are still
valid for the general case of lateral velocity variations.
However, the magnitude of the error introduced by the
mispositioning of sources and receivers at depth when evaluating
the velocity function cannot be neglected in principle.
These errors are dependent on the spatial variability of
the velocity function, and cannot be readily analyzed analytically.
In the following section we show accurate migration results
obtained over a velocity function varying both laterally
and vertically. These results are encouraging and
suggest that the range of application of common-azimuth
migration to depth migration problems is fairly large.
 |
MIGRATION RESULTS
We tested common-azimuth migration by imaging
two synthetic data sets generated by a modeling
program based on the Kirchhoff integral.
The Green functions are
computed analytically assuming
velocity functions with a constant spatial gradient.
In both cases the velocity at the origin of the spatial
coordinates is equal to ![]() .The first data set is generated assuming
a vertical gradient of
.The first data set is generated assuming
a vertical gradient of ![]() while
the second data set is generated assuming a gradient with the horizontal
component equal to
while
the second data set is generated assuming a gradient with the horizontal
component equal to ![]() and the vertical component equal to
and the vertical component equal to
![]() .
The horizontal component of the gradient
is oriented at an angle of 45 degrees with respect to the
offset azimuth (in-line direction) of the acquisition geometry.
The reflectivity model is a constant reflectivity
function positioned along a half-spherical dome superimposed
onto a horizontal planar reflector.
.
The horizontal component of the gradient
is oriented at an angle of 45 degrees with respect to the
offset azimuth (in-line direction) of the acquisition geometry.
The reflectivity model is a constant reflectivity
function positioned along a half-spherical dome superimposed
onto a horizontal planar reflector.
The acquisition geometry has 128 midpoint along both the in-line
and cross-line directions;
with midpoint spacing of ![]() in both directions.
Each midpoint gather has 64 offsets, spaced every
in both directions.
Each midpoint gather has 64 offsets, spaced every ![]() ;
the nearest offset traces are actually recorded at zero offset.
The offset-azimuth of the data is aligned with the in-line
direction.
Figure
;
the nearest offset traces are actually recorded at zero offset.
The offset-azimuth of the data is aligned with the in-line
direction.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) show two in-line
zero-offset sections
extracted from respectively the vertical gradient data set
and the oblique gradient data set.
The effects of the lateral component of the velocity gradient
are evident in both the tilting of the horizontal reflector,
and in the asymmetry of the quasi-hyperbolic
reflections from the dome.
show two in-line
zero-offset sections
extracted from respectively the vertical gradient data set
and the oblique gradient data set.
The effects of the lateral component of the velocity gradient
are evident in both the tilting of the horizontal reflector,
and in the asymmetry of the quasi-hyperbolic
reflections from the dome.
Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) show
an in-line section and a depth slice of the results of
migrating the vertical gradient data set.
The in-line section (Figure
show
an in-line section and a depth slice of the results of
migrating the vertical gradient data set.
The in-line section (Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is taken across the
middle of the dome, while the depth slice (Figure
) is taken across the
middle of the dome, while the depth slice (Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
is taken across the base of the dome
)
is taken across the base of the dome ![]() .Common-azimuth migration has accurately imaged the data;
both the in-line section
and the depth slice show a perfect focusing of the reflectors.
To visually verify the isotropic response of common-azimuth
migration we overlaid a circle onto the depth slice.
The migrated dome is perfectly circular,
notwithstanding the ray bending
caused by the strong vertical velocity gradient.
.Common-azimuth migration has accurately imaged the data;
both the in-line section
and the depth slice show a perfect focusing of the reflectors.
To visually verify the isotropic response of common-azimuth
migration we overlaid a circle onto the depth slice.
The migrated dome is perfectly circular,
notwithstanding the ray bending
caused by the strong vertical velocity gradient.
Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) show
the result of migrating the oblique gradient data set.
The in-line section (Figure
show
the result of migrating the oblique gradient data set.
The in-line section (Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
shows that common-azimuth migration
has correctly positioned the reflectors.
The planar reflector has been flattened, and the spherical
dome has been properly focused.
A spatial variability in both the frequency content
and the amplitude of the migrated reflector is noticeable
in the depth slice.
The frequency variability is expected,
and it is caused by the widening of the spatial
wavelength of the wavefield caused by higher propagation
velocities.
The wavelet is narrower closer to the origin (upper-left corner)
where velocity is lower
and it is wider where the velocity is higher (lower-right corner).
The amplitude variations cannot be readily
explained, and further analysis is needed to determine
whether they are artifacts of common-azimuth migration.
The combined frequency and amplitude effects
creates an ``anisotropic'' appearance to the migrated image.
However, by overlaying
a circle onto the plot of the seismic data
we see that the migrated dome, though not perfectly
circular, it is very close to circular.
The comparison of these
results with the results from the vertical gradient data set
confirm the accuracy of common-azimuth migration even
in the presence of strong lateral velocity gradients.
)
shows that common-azimuth migration
has correctly positioned the reflectors.
The planar reflector has been flattened, and the spherical
dome has been properly focused.
A spatial variability in both the frequency content
and the amplitude of the migrated reflector is noticeable
in the depth slice.
The frequency variability is expected,
and it is caused by the widening of the spatial
wavelength of the wavefield caused by higher propagation
velocities.
The wavelet is narrower closer to the origin (upper-left corner)
where velocity is lower
and it is wider where the velocity is higher (lower-right corner).
The amplitude variations cannot be readily
explained, and further analysis is needed to determine
whether they are artifacts of common-azimuth migration.
The combined frequency and amplitude effects
creates an ``anisotropic'' appearance to the migrated image.
However, by overlaying
a circle onto the plot of the seismic data
we see that the migrated dome, though not perfectly
circular, it is very close to circular.
The comparison of these
results with the results from the vertical gradient data set
confirm the accuracy of common-azimuth migration even
in the presence of strong lateral velocity gradients.
 |
 |
 |
 |
 |
 |
CONCLUSIONS We have shown that common-azimuth migration () can be successfully applied to imaging 3-D prestack data with laterally varying velocity. This important generalization of common-azimuth migration was made possible by two theoretical insights. The first one led us to recast common-azimuth migration as a recursive application of a new common-azimuth downward continuation operator. The second one is a ray-theoretical interpretation of common-azimuth downward continuation that enables us to analyze the errors in presence of ray bending caused by velocity inhomogeneities.
We implemented common-azimuth depth migration by downward continuation in mixed space-wavenumber domain using a split-step scheme. The application of our depth migration algorithm to a data set with a strong horizontal component of the velocity gradient resulted in an accurate imaging of the reflectors. ACKNOWLEDGEMENTS We thank Arnaud Berlioux for helping to generate the dome model using GOCAD. Biondo Biondi would like to thank Norm Bleistein for a short conversation that motivated him to better understand the errors involved in the stationary-phase derivation of common-azimuth migration.
[SEP,res]
A
The purpose of this Appendix is
to demonstrate the equivalence of the stationary phase derivation
of the common-azimuth downward continuation operator
[equation (7) in the main text] and
the constraint on the propagation directions
of the source rays
![]() and receiver rays
and receiver rays
![]() expressed in equation (8).
expressed in equation (8).
We start by showing that equation (8) is directly derived by imposing the condition that the source ray and the receiver ray lie on the same plane. For this condition to be fulfilled, the components of the two rays in the direction of the cross-line axis y must be equal. From elementary geometry, these components are
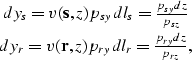 |
||
| (14) |
| |
(15) |
The second step is to eliminate psz and prz from equation (A-2) by using the following relationships among the ray parameters
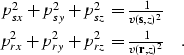 |
||
| (16) |
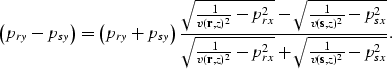 |
(17) |
To derive equation (7) from equation (A-4) it is sufficient to substitute for the ray parameters by applying the relationships
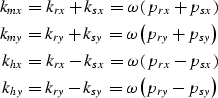 |
||