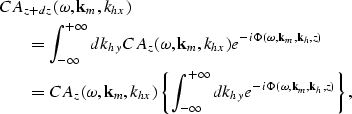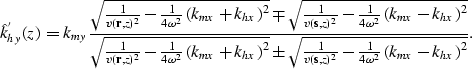![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)


Next: Geometric interpretation of common-azimuth
Up: Table of Contents
3-D prestack depth migration of common-azimuth data
Biondo Biondi and Gopal Palacharla
biondo@sep.stanford.edu, gopal@sep.stanford.edu
ABSTRACT
We extended the common-azimuth 3-D prestack migration
method presented in a previous report
() to the important case
of imaging common-azimuth data
when the velocity field varies laterally.
This generalization leads to an efficient
mixed space-wavenumber domain algorithm
for 3-D prestack depth migration of common-azimuth data.
We implemented the method using a split-step scheme,
and applied it to the migration of two synthetic
data sets: the first data set was generated assuming a vertical velocity
gradient,
the second one assuming a velocity gradient with both
a vertical and a horizontal component.
Common-azimuth migration correctly imaged the reflectors in both cases.
|
INTRODUCTION
For 3-D prestack migration,
Kirchhoff methods are usually preferred over methods based on
recursive downward continuation
because of their flexibility in
handling 3-D prestack data geometries ().
Kirchhoff methods can be employed to efficiently migrate data sets
with uneven spatial sampling and
data sets that are subsets of the complete prestack data,
such as common-offset cubes and common-azimuth cubes.
For recursive methods the irregular sampling problem can be
addressed with an interpolation preprocessing step,
though in practice it can be a challenging task.
However, in principle the downward continuation of prestack subsets
should be carried out in the full 5-D data space,
even when the original subset is 3-D (common offset) or 4-D (common azimuth).
As a result of these constraints on the dimensionality
of the computational domain, most of the computations
are wasted on propagating components of the wavefield that either are equal
to zero or do not contribute to the final image.
These potential limitations of recursive methods have led
the industry to adopt almost exclusively Kirchhoff methods
for 3-D prestack migration
(, ),
though recursive methods have some intrinsic advantages over
Kirchhoff methods.
First, they are potentially more accurate and robust because
they are based on the full wave-equation and not on an asymptotic
solution based on ray theory.
Second, when they can be used to extrapolate the recorded data without
increasing their dimensionality (e.g. zero-offset data), they can
be implemented more efficiently than the corresponding Kirchhoff methods.
acquis
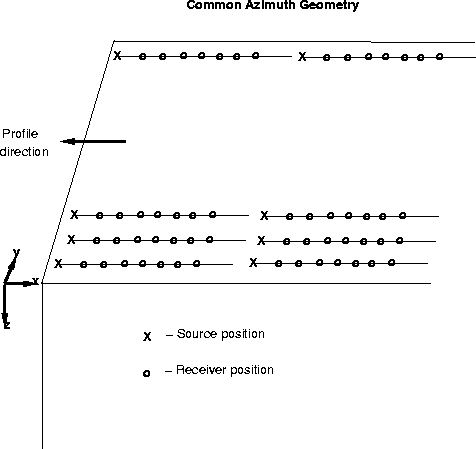
Figure 1 Schematic showing the acquisition geometry of common-azimuth data.
The data are acquired along parallel lines, with all the offset
vectors aligned along a common azimuth.
For simplicity, but without loss of generality,
we assume that the common offset-azimuth is aligned along the in-line
direction.

In a previous report ()
we introduced a method for efficiently
migrating common-azimuth data
(see Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) for a schematic representation
of common-azimuth acquisition geometry)
by recursive downward continuation in the original 4-D space.
An efficient algorithm for migrating common-azimuth subsets has useful
practical applications because common-azimuth data are either the result
of a collection of actual physical experiments
(e.g. single-streamer marine survey with negligible cable feather)
or they may be synthesized by preprocessing
().
However, in the previous report we applied common-azimuth
migration to the case of limited interest when velocity varies only with depth;
we did not address the important issue
of applying the method to the general case when the
velocity function is laterally varying.
Similarly, Ikelle developed
(unknown to us at the time we wrote the first report)
a linearized inversion method for common-azimuth data
that shares with our previous work the same theoretical basis,
but also shares the same limitations of applicability
to a medium with only vertical velocity variations.
In this paper, we overcome these limitations and we
generalize common-azimuth migration to
the case of laterally varying velocity.
for a schematic representation
of common-azimuth acquisition geometry)
by recursive downward continuation in the original 4-D space.
An efficient algorithm for migrating common-azimuth subsets has useful
practical applications because common-azimuth data are either the result
of a collection of actual physical experiments
(e.g. single-streamer marine survey with negligible cable feather)
or they may be synthesized by preprocessing
().
However, in the previous report we applied common-azimuth
migration to the case of limited interest when velocity varies only with depth;
we did not address the important issue
of applying the method to the general case when the
velocity function is laterally varying.
Similarly, Ikelle developed
(unknown to us at the time we wrote the first report)
a linearized inversion method for common-azimuth data
that shares with our previous work the same theoretical basis,
but also shares the same limitations of applicability
to a medium with only vertical velocity variations.
In this paper, we overcome these limitations and we
generalize common-azimuth migration to
the case of laterally varying velocity.
The generalization of common-azimuth migration
presented in this paper is based on two new theoretical insights.
First, we derive common-azimuth migration as a recursive
downward continuation by a new operator
that continues common-azimuth data recorded at one
depth level to common-azimuth data recorded at the next depth level.
The previous derivation of common-azimuth migration
was based on stationary-phase approximation to
the whole process of downward continuation
followed by imaging at zero offset.
Isolating the common-azimuth downward continuation from
imaging enables us to better understand the
assumptions underlying common-azimuth migration.
The second improvement in the theory follows
from a ray-based geometric interpretation of common-azimuth
downward continuation.
Thanks to this ray interpretation we derived and justified
a more general formulation of the stationary-phase
result that can be applied to downward continuation
in presence of lateral velocity variations.
Furthermore, the geometric insight enables us
to analyze the errors caused by the
use of common-azimuth continuation in place of
full 3-D prestack continuation and to gain an appreciation of
the limitations and strengths of the proposed method.
COMMON-AZIMUTH DOWNWARD CONTINUATION
We first derive a wave-equation operator for
downward continuing common-azimuth data
by applying a stationary phase
approximation to the frequency-wavenumber
domain formulation of the full 3-D prestack downward continuation
operator.
Then, we present a ray-based geometric interpretation
of the stationary-phase result, and use this
geometric interpretation to generalize the frequency-wavenumber
results to a medium where the velocity function varies laterally,
and to analyze the errors caused by the use of common-azimuth
continuation in the presence of lateral velocity variations.
The acquisition geometry of common-azimuth data is shown
in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
Without loss of generality we assume
that the common offset-azimuth is aligned with the x axis (in-line axis).
Since the offset vectors between source and receivers are constrained to
have the same azimuth, common-azimuth data has only four dimensions.
The four axes are: recording time, two midpoints,
and the offset along the azimuthal direction.
A common azimuth data set can be downward continued by applying
the full 3-D prestack downward continuation operator,
that in the frequency-wavenumber domain can be expressed
as a phase-shift operator, with the phase given by
the 3-D double square root equation (DSR).
In 3-D the DSR equation is a function of five scalar variables:
the temporal frequency (
.
Without loss of generality we assume
that the common offset-azimuth is aligned with the x axis (in-line axis).
Since the offset vectors between source and receivers are constrained to
have the same azimuth, common-azimuth data has only four dimensions.
The four axes are: recording time, two midpoints,
and the offset along the azimuthal direction.
A common azimuth data set can be downward continued by applying
the full 3-D prestack downward continuation operator,
that in the frequency-wavenumber domain can be expressed
as a phase-shift operator, with the phase given by
the 3-D double square root equation (DSR).
In 3-D the DSR equation is a function of five scalar variables:
the temporal frequency (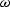 ),
the two components of the midpoint wavenumber
vector
),
the two components of the midpoint wavenumber
vector 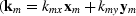 ),
and the two components of the offset wavenumber
evaluation of
the phase function
),
and the two components of the offset wavenumber
evaluation of
the phase function 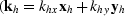 ).
The downward continuation of common-azimuth
).
The downward continuation of common-azimuth 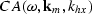 data from
depth z to depth z+ dz by full 3-D prestack continuation can be
expressed as
data from
depth z to depth z+ dz by full 3-D prestack continuation can be
expressed as
| 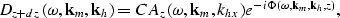 |
(1) |
where the phase function is given by
| 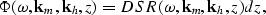 |
(2) |
and the double-square root equation is equal to
| ![\begin{eqnarray}
\lefteqn{DSR(\omega,{\bf k}_{m},{\bf k}_{h},z^{})} \nonumber \\...
...k_{mx}-k_{hx}\right)^2 + \left(k_{my}-k_{hy}\right)^2 ]} \right\},\end{eqnarray}](img7.gif) |
|
| |
| (3) |
where 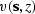 and
and 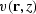 are the velocities evaluated respectively
at the source and receiver locations at depth z.
The distinction between velocity at the source and velocity at the receiver
may seem somewhat artificial in the wavenumber domain,
but it is important to keep them as two separate parameters during
the stationary-phase approximation to derive a
method applicable to depth migration.
A physical interpretation of the significance
of the source and receiver velocity terms is possible
after the geometric interpretation of the stationary-phase
results presented in the next section.
are the velocities evaluated respectively
at the source and receiver locations at depth z.
The distinction between velocity at the source and velocity at the receiver
may seem somewhat artificial in the wavenumber domain,
but it is important to keep them as two separate parameters during
the stationary-phase approximation to derive a
method applicable to depth migration.
A physical interpretation of the significance
of the source and receiver velocity terms is possible
after the geometric interpretation of the stationary-phase
results presented in the next section.
The result of the downward continuation with the full 3-D prestack
is five dimensional, although the original common-azimuth data
is only four dimensional.
This increase in the dimensionality of the computational domain
causes a drastic increase in the computational and memory requirements
of 3-D prestack downward continuation, making it unattractive
compared with other migration methods, such as the ones based on the
Kirchhoff integral.
However, the computational cost can be greatly reduced by
applying a new downward continuation operator
that evaluates the wavefield at the new depth level
only along the offset-azimuth of the original data.
We derive this operator by
evaluating the data
at the new depth level 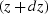 at the origin of the cross-line offset axis
at the origin of the cross-line offset axis 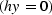 by integration over the cross-line offset wavenumber,
by integration over the cross-line offset wavenumber,
| 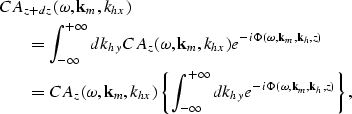 |
|
| |
| (4) |
and by recognizing that since
common-azimuth data is independent of khy
the integral can be pulled inside
and analytically approximated by the stationary
phase method ().
The common-azimuth downward continuation operator can thus be written as
| 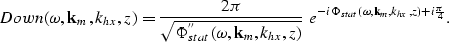 |
(5) |
The phase function
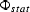 is equal to the phase function in
equation (2)
evaluated along the stationary path, and is equal to
is equal to the phase function in
equation (2)
evaluated along the stationary path, and is equal to
| ![\begin{displaymath}
\Phi_{stat}(\omega,{\bf k}_{m},k_{hx},{z})= DSR \left [ \omega,{\bf k}_{m},k_{hx},k_{hy}^{'}{({z})},z^{}\right ]dz^{};\end{displaymath}](img15.gif) |
(6) |
where
and khy'(z) is the stationary path for the
double-square root equation, as a function of khy.
There are two solutions for the stationary path of the double-square root
equation; they are
| 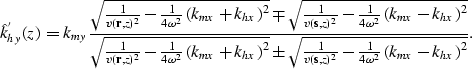 |
(7) |
In choosing between these two solutions,
we first notice that one solution is the inverse of the other.
Second we consider the limiting case of the in-line offset
wavenumber (khx) equal to zero.
In this case one solution diverges while the other
(being the one with the minus sign at the numerator) is equal to zero.
We accept this second solution because it is consistent with the
notion that when both khx and khy vanish the
double square root equation reduces to the single square root equation
that is commonly used for migrating zero-offset
data ().
The implementation of common-azimuth downward continuation
as described by equation (3)
through equation (7) yields an algorithm for
efficient migration of common-azimuth data.
When the velocity field is only a function of depth
the method can be efficiently implemented by a simple
phase-shift algorithm.
When the velocity field is also function of the lateral coordinates,
and accurate depth-migration is required, the method
should be implemented using a mixed space-wavenumber
domain migration scheme,
such as Phase-Shift Plus Interpolation (PSPI) ()
or split step ().
We implemented the equations using a straightforward
generalization of split step to prestack migration
because of its simplicity and computational efficiency;
other choices would have probably been just as effective.
In the next two sections, we analyze
common-azimuth downward continuation
by using a ray-theoretical interpretation of the method.
The goal is to understand the underlying assumptions,
and to understand the accuracy limitation of the method
when velocity variations cause ray bending.


![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)


Next: Geometric interpretation of common-azimuth
Up: Table of Contents
Stanford Exploration Project
5/9/2001
![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif)
![\begin{eqnarray}
\lefteqn{DSR(\omega,{\bf k}_{m},{\bf k}_{h},z^{})} \nonumber \\...
...k_{mx}-k_{hx}\right)^2 + \left(k_{my}-k_{hy}\right)^2 ]} \right\},\end{eqnarray}](img7.gif)