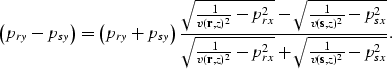Next: Common-azimuth downward continuation and
Up: Biondi & Palacharla: 3-D
Previous: Biondi & Palacharla: 3-D
The common-azimuth downward continuation operator derived
by stationary phase has a straightforward geometric interpretation
in terms of propagation directions of the rays of the continued wavefield.
In Appendix A we show that expression for the stationary path
of equation (7) is equivalent to the
relationship
| 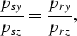 |
(8) |
among the ray parameters for the rays downward
propagating the sources
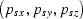 and the ray parameters for the rays
downward propagating the receivers
and the ray parameters for the rays
downward propagating the receivers
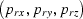 .This relationship between the ray parameters constrains
the direction of propagation of the source and receiver rays,
for each possible pair of rays.
In particular, the source ray and the receiver ray must lie on the same plane;
with all the possible propagation planes sharing the line that connects
the source and receiver location at each depth level.
This geometric relationship
constrains the sources and receivers at the new depth level
to be aligned along the same azimuth as the source and receivers
at the previous depth level,
consistently with the condition that we imposed
for the stationary phase derivation of the common-azimuth
downward continuation operator [equation (4)].
Figure
.This relationship between the ray parameters constrains
the direction of propagation of the source and receiver rays,
for each possible pair of rays.
In particular, the source ray and the receiver ray must lie on the same plane;
with all the possible propagation planes sharing the line that connects
the source and receiver location at each depth level.
This geometric relationship
constrains the sources and receivers at the new depth level
to be aligned along the same azimuth as the source and receivers
at the previous depth level,
consistently with the condition that we imposed
for the stationary phase derivation of the common-azimuth
downward continuation operator [equation (4)].
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows a graphical representation
of the geometric interpretation of common-azimuth downward
continuation. The source ray and the receiver ray must lie
on any of the slanted planes that share the line
connecting the source and receiver locations.
shows a graphical representation
of the geometric interpretation of common-azimuth downward
continuation. The source ray and the receiver ray must lie
on any of the slanted planes that share the line
connecting the source and receiver locations.
In Appendix A we show that from equation (8)
it is possible to derive
the ray parameter equivalent of the stationary-path
expression of equation (7); that is,
| 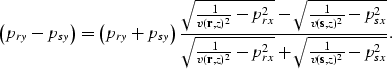 |
(9) |
In this expression the distinction between the
velocity at the source location,
and the velocity at the receiver location introduced
in equation (3), and formally carried through
the stationary phase approximation, is now physically meaningful.
It implies that the source rays and receiver rays
must lie on the same plane,
notwithstanding different local velocities and ray bending.





Next: Common-azimuth downward continuation and
Up: Biondi & Palacharla: 3-D
Previous: Biondi & Palacharla: 3-D
Stanford Exploration Project
5/9/2001
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows a graphical representation
of the geometric interpretation of common-azimuth downward
continuation. The source ray and the receiver ray must lie
on any of the slanted planes that share the line
connecting the source and receiver locations.
shows a graphical representation
of the geometric interpretation of common-azimuth downward
continuation. The source ray and the receiver ray must lie
on any of the slanted planes that share the line
connecting the source and receiver locations.