DMO and NMO

The Dip Moveout correction (DMO) is in fact an extension to the NMO correction when dips are present. In the presence of only horizontal layers NMO tries to correct the effect of the offset and transform all the constant-offset section into zero-offset section. You can understand the DMO correction as doing exactly the same thing not only for horizontal events but also for dipping events. DMO is an intermediate processing step which attempts to position the conflicting dips in the correct zero-offset location such that after NMO, CMP stacking will not attenuate crossing events.

These concepts are all formulated for a constant velocity medium. For a variable velocity medium the transformation from constant-offset to zero-offset performed by NMO combined with DMO can not be split into two separate processes; instead it forms a single step process called Migration to Zero-Offset (MZO). In constant velocity media $MZO = NMO \cdot DMO$.

To define the parameters involved in the DMO correction we need to analyze the kinematics of the constant-offset reflection of a dipping layer. For a horizontal layer, the reflection point is situated right under the location of the common-midpoint (CMP). For the dipping layer sketched in Figure the reflection point for the source-receiver ray is R. This point is positioned updip relative to the intersection O of the zero-offset ray from the common-midpoint F with the dipping reflector.

In a constant-offset section the trace corresponding to a source positioned at point A and a receiver positioned at point B is placed in the location of the CMP. However in a zero-offset experiment the reflection point R is observed from the surface position J. Migration to zero-offset $(NMO \cdot DMO)$ is the transformation which relocates a reflection point as seen in constant-offset to a place corresponding to the reflection point as seen in zero-offset.

 

dmofig2
Figure 4 DMO kinematics. A dipping reflector in a constant velocity medium.
The dipping angle is $\theta$.The raypath from the source to the receiver is sketched by the segments AR and RB. The reflection point R is seen in the zero-offset case from the surface point J. The zero-offset raypath from J is equal to the segment JK. The incidence angle at R is i.

In order to define the operator we have to calculate the time correction and the surface coordinate correction to transform a constant-offset section into a zero-offset section. In Figure the segment JR represents the zero-offset ray from the reflection point R. The segment FJ represents the surface correction from the CMP to the real zero-offset position of both the source and receiver. We can calculate the surface correction and the traveltime correction using some elementary geometry.

The source-receiver traveltime t_h corresponds to the ray path ARB. The velocity of the medium is v and the constant-offset traveltime is

$$t_h = {{({\bf AR} + {\bf RB})} \over v }.$$

The segment AB represents the offset between the source and receiver and we have

$${\bf AF} ={\bf FB} = {{\bf AB} \over 2} = h .$$

The segment AC is equal to AR +RB and therefore ${\bf AC} = v t_h$.

From Figure we observe that the most important equation relating the angle of the dipping reflector and the incidence angle of the constant-offset raypath is  

$${2h \cos \theta} = {v t_h \sin i} = {\bf EC},$$ (4)

where $\theta$ is the dipping angle of the reflector and i is the incident angle of the constant-offset raypath at the reflection point R. From equation (4) we have

$$\cos i = {1 \over {v t_h}} \sqrt {(v t_h)^2-(2h\cos\theta)^2}.$$

To calculate the segment $x_0={\bf FJ}$ which is the DMO surface correction we note that

$$x_0 = {{\bf OR} \over { \cos \theta}}$$

and

$${\bf OR} = {\bf MO} \tan i .$$

The segment MN= 2MO is easily calculated as half the difference between the bases of the trapezoid ABCD. We have  

$${\bf MO} = { {\bf MN} \over 2} = { {{\bf AD} - {\bf BC}} \over 4} = h \sin \theta$$ (5)

and finally  

$$x_0 = {h \sin \theta }{{\tan i} \over {\cos \theta}}= { {2h^2 \sin \theta} \over { \sqrt {(v t_h)^2-(2h\cos\theta)^2}}}.$$ (6)

Knowing segment FJ, the zero-offset traveltime given by the segment JK is calculated as

$${\bf JK} = { {\bf FG} - 2 {\bf FJ} \sin \theta}.$$

The segment FG is expressed in equation (1)

$${\bf FG} = {\sqrt { (v t_h)^2 - (2 h \cos \theta )^2}}.$$

Therefore we have  

$$t_0={ {\bf JK} \over v} = {{(vt_h)^2-(2h)^2} \over {v \sqrt {(v t_h)^2-(2h\cos\theta)^2}}}.$$ (7)

We have obtained the parametric equations defining the $NMO \cdot DMO$ operator in constant velocity media:  

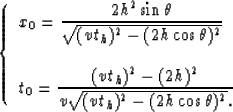$$\left \{ \begin{array} {l} x_0 = \displaystyle{ {2h^2 \sin \... ... {v \sqrt {(v t_h)^2-(2h\cos\theta)^2} }. }\end{array} \right.$$ (8)

The formulas in equation () tell us where an event from a constant-offset section is moved in a zero-offset section when the dip is known. However we will see later that the dip doesn't have to be known to correctly apply the DMO operator. Figure shows the variation of t₀ and x₀ for a whole range of dips. For a zero dip we have

$$\left \{ \begin{array} {l} x_0 = \displaystyle{ 0 } \\ \\ t_... ...^2 - \left ( {{2h} \over v} \right )^2 } }\end{array} \right.$$

which is just the NMO correction.

 

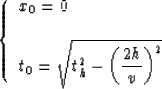
MZOimpulse Figure 5 The distribution of the DMO correction for all dips $( { {-\pi \over 2} \leq \theta \leq {\pi \over 2} })$.