




Next: DMO and NMO
Up: Introduction
Previous: The need for DMO
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows a dipping reflector and the
position of the source, geophone and CMP.
The constant-offset traveltime from the source
at point A to the receiver at point B
is represented by the segments AR+RB.
The zero-offset traveltime from the CMP
to the reflector and back is given by the
segment FG.
The dipping reflector serves as the axis of symmetry for
the figure.
dmofig1
shows a dipping reflector and the
position of the source, geophone and CMP.
The constant-offset traveltime from the source
at point A to the receiver at point B
is represented by the segments AR+RB.
The zero-offset traveltime from the CMP
to the reflector and back is given by the
segment FG.
The dipping reflector serves as the axis of symmetry for
the figure.
dmofig1
Figure 3 A dipping reflector in a constant velocity medium. The
dipping angle is 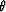 . The raypath from the source
to the receiver is sketched by the segments AR and
RB. The zero-offset raypath is equal to the
segment FG.
. The raypath from the source
to the receiver is sketched by the segments AR and
RB. The zero-offset raypath is equal to the
segment FG.

For the geometry in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) we have
we have
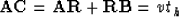
where v is the velocity of the medium and th is the
shot-receiver traveltime. The segment FG (which has the length
of the zero-offset raypath) is
equal to the segment AE.
From Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif)
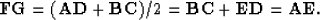
From the triangle
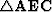 we have
we have
| 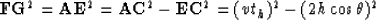 |
(1) |
where 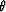 is the angle of the dipping reflector and
2h is the distance between source and receiver.
Finally,
by dividing the segments with the velocity we have
the zero-offset traveltime from the CMP to the reflector:
is the angle of the dipping reflector and
2h is the distance between source and receiver.
Finally,
by dividing the segments with the velocity we have
the zero-offset traveltime from the CMP to the reflector:
| 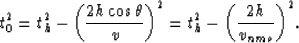 |
(2) |
From equation (2) we easily see that the
expression for th is a hyperbola, with the
top at t0. The NMO
velocity necessary to flatten the hyperbola for a dipping
reflector is
| 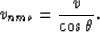 |
(3) |





Next: DMO and NMO
Up: Introduction
Previous: The need for DMO
Stanford Exploration Project
11/18/1997
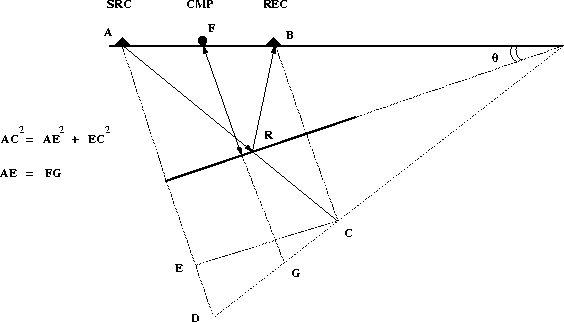
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows a dipping reflector and the
position of the source, geophone and CMP.
The constant-offset traveltime from the source
at point A to the receiver at point B
is represented by the segments AR+RB.
The zero-offset traveltime from the CMP
to the reflector and back is given by the
segment FG.
The dipping reflector serves as the axis of symmetry for
the figure.
shows a dipping reflector and the
position of the source, geophone and CMP.
The constant-offset traveltime from the source
at point A to the receiver at point B
is represented by the segments AR+RB.
The zero-offset traveltime from the CMP
to the reflector and back is given by the
segment FG.
The dipping reflector serves as the axis of symmetry for
the figure.

![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) we have
we have
![]()
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif)
![]()