Next: Problem 1.
Up: Introduction
Previous: DMO and NMO
The goal of the  processing step is to transform
a constant-offset section into a zero-offset section.
We can conceive any structure (or depth model)
as composed of independent diffractors. This
is the commonplace assumption for Kirchhoff migration.
By summing the contributions from all the
diffractors we can obtain our constant-offset section.
Following this hypothesis it is interesting to examine
the behavior of a single diffraction curve in constant-offset.
Figure
processing step is to transform
a constant-offset section into a zero-offset section.
We can conceive any structure (or depth model)
as composed of independent diffractors. This
is the commonplace assumption for Kirchhoff migration.
By summing the contributions from all the
diffractors we can obtain our constant-offset section.
Following this hypothesis it is interesting to examine
the behavior of a single diffraction curve in constant-offset.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows a constant-offset diffraction
curve together with a zero-offset diffraction curve which
is actually a hyperbola. The aim of the
shows a constant-offset diffraction
curve together with a zero-offset diffraction curve which
is actually a hyperbola. The aim of the  step
is to transform the former into the latter.
step
is to transform the former into the latter.
cozo
Figure 6 Zero-offset hyperbola and the
constant-offset diffraction curve.
|
| 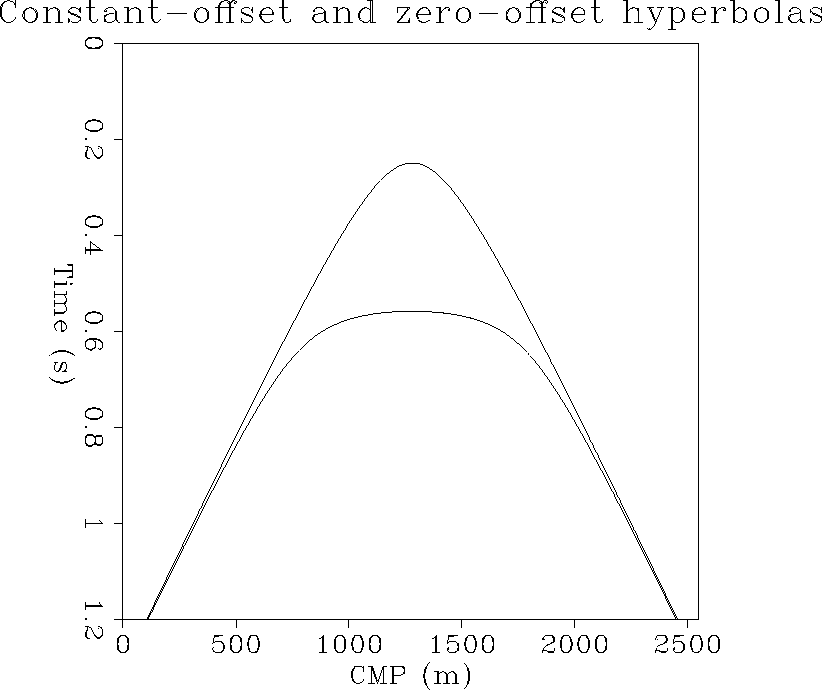 |

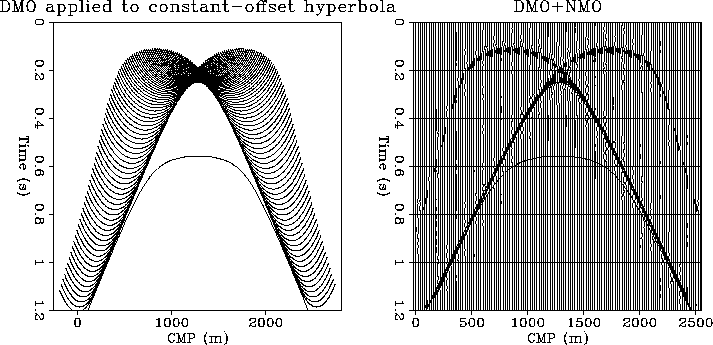
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the kinematics of the
shows the kinematics of the 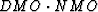 operator; each point along the constant-offset diffraction
curve is spread along an operator similar to the one shown in
Figure
operator; each point along the constant-offset diffraction
curve is spread along an operator similar to the one shown in
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and using equation (8).
The result of this operation is
displayed on the right side in Figure
and using equation (8).
The result of this operation is
displayed on the right side in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . The
artifacts at the top of the figure are due to the
constant amplitude assigned along the DMO curve. In
reality the amplitude along the DMO curve is tapered
toward the end of the operator, as will be shown
in the next chapters.
. The
artifacts at the top of the figure are due to the
constant amplitude assigned along the DMO curve. In
reality the amplitude along the DMO curve is tapered
toward the end of the operator, as will be shown
in the next chapters.
codmo
Figure 7 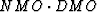 transforms a constant-offset diffraction curve to
a zero-offset hyperbola.
transforms a constant-offset diffraction curve to
a zero-offset hyperbola.
(LEFT) 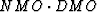 kinematics; each
point on the constant-offset diffraction curve is spread along
the DMO curve and shifted with the NMO correction.
kinematics; each
point on the constant-offset diffraction curve is spread along
the DMO curve and shifted with the NMO correction.
(RIGHT) The result of applying 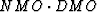 to the constant-offset hyperbola.
The artifacts are due to using a constant amplitude along the DMO curve.
to the constant-offset hyperbola.
The artifacts are due to using a constant amplitude along the DMO curve.






Next: Problem 1.
Up: Introduction
Previous: DMO and NMO
Stanford Exploration Project
11/18/1997

![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows a constant-offset diffraction
curve together with a zero-offset diffraction curve which
is actually a hyperbola. The aim of the
shows a constant-offset diffraction
curve together with a zero-offset diffraction curve which
is actually a hyperbola. The aim of the 
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the kinematics of the
shows the kinematics of the ![]() operator; each point along the constant-offset diffraction
curve is spread along an operator similar to the one shown in
Figure
operator; each point along the constant-offset diffraction
curve is spread along an operator similar to the one shown in
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and using equation (8).
The result of this operation is
displayed on the right side in Figure
and using equation (8).
The result of this operation is
displayed on the right side in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . The
artifacts at the top of the figure are due to the
constant amplitude assigned along the DMO curve. In
reality the amplitude along the DMO curve is tapered
toward the end of the operator, as will be shown
in the next chapters.
. The
artifacts at the top of the figure are due to the
constant amplitude assigned along the DMO curve. In
reality the amplitude along the DMO curve is tapered
toward the end of the operator, as will be shown
in the next chapters.