The mapping functions for the time-to-depth conversion are previously computed by tracing image rays. The method gives the mapping functions along the image rays. Mapping time-migrated image along the image rays subsequently gives the depth-migrated image that has to be interpolated onto a regular grid. For complicated velocity models, image ray may cross each other or not penetrate shadow zones; the interpolation is thus cumbersome and computationally expensive. In this section, I describe an efficient algorithm for computing the mapping functions of the image-ray corrections on a regular grid,
To compute the functions ![]() and
and ![]() in equation (1), we
consider two partial differential equations. Because all image rays
shoot vertically when leaving the surface, they are associated with
a vertically incident plane wavefront. The value of function
in equation (1), we
consider two partial differential equations. Because all image rays
shoot vertically when leaving the surface, they are associated with
a vertically incident plane wavefront. The value of function
![]() is the
traveltime for the wavefront to propagate from the surface to a subsurface
point (x,z), which satisfies the eikonal equation:
is the
traveltime for the wavefront to propagate from the surface to a subsurface
point (x,z), which satisfies the eikonal equation:
| |
(12) |
| |
(13) |
Two partial differential equations (12) and (13) can be solved simultaneously by using an up-wind finite difference method (Zhang, 1991), and the results are samples of the two mapping functions on a regular grid. Thus, the image-ray corrections can be implemented with an algorithm summerized, as follow:
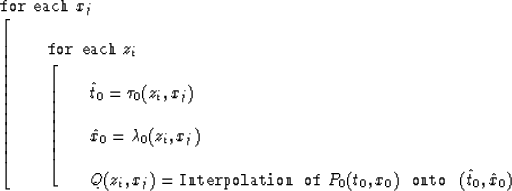
The functions ![]() and p(x,z;xs) in equations (6)
and (11) can be computed in a similar way. Two partial
differential equations
and p(x,z;xs) in equations (6)
and (11) can be computed in a similar way. Two partial
differential equations
| |
(14) |
| |
(15) |