




Next: Constant offset imaging
Up: GENERALIZED IMAGE-RAY METHOD
Previous: GENERALIZED IMAGE-RAY METHOD
Let us first study the generalized image-ray method for profile imaging.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the ray paths in a common shot experiment.
The seismic energy generated by a shot at surface location xs propagates
towards a point scatterer at subsurface position (x,z).
After being diffracted from the scatterer, the energy travels along the multiple
ray paths connecting the scatterer to each receiver of a receiver array.
On the recorded shot gather, the seismic
energy is distributed in the data samples along a diffraction curve
that is determined by the functional relationship between traveltime t and
receiver location xr. The diffraction curve has a hyperbolic shape
when the overburden velocities of the scatterer are free of lateral variations.
If we assume that the lateral velocity variations are confined
to a reasonable scale, this curve usually is well fit by a hyperbola
in the vicinity of its apex. Consequently, a profile time-migration
can collapse the energy distributed over this portion of the diffraction curve.
imraycsg
shows the ray paths in a common shot experiment.
The seismic energy generated by a shot at surface location xs propagates
towards a point scatterer at subsurface position (x,z).
After being diffracted from the scatterer, the energy travels along the multiple
ray paths connecting the scatterer to each receiver of a receiver array.
On the recorded shot gather, the seismic
energy is distributed in the data samples along a diffraction curve
that is determined by the functional relationship between traveltime t and
receiver location xr. The diffraction curve has a hyperbolic shape
when the overburden velocities of the scatterer are free of lateral variations.
If we assume that the lateral velocity variations are confined
to a reasonable scale, this curve usually is well fit by a hyperbola
in the vicinity of its apex. Consequently, a profile time-migration
can collapse the energy distributed over this portion of the diffraction curve.
imraycsg
Figure 1 Ray paths in a common shot experiment. The solid line shows an image ray.

If time migration is implemented by using a Kirchhoff summation,
the time-image sample at (t0,x0) is
the weighted sum of data samples along a migration curve,
as follows:
| 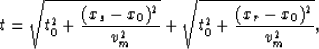 |
(3) |
where vm is a migration velocity.
For a given shot location xs, this equation defines traveltime t
as a function of receiver location xr.
By taking the derivative of traveltime t in equation (3)
with respect to receiver location xr and setting the result to zero,
we can find the coordinates of the apex of the migration curve for given
(t0,x0), as follows:
| 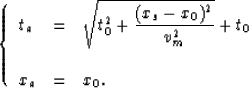 |
(4) |
Thus, the Kirchhoff time-migration focuses the diffracted energy
along the diffraction curve whose apex is at (ta,xa) to the point
(t0,x0) of the time-migrated image.
The correct time-to-depth conversion should map the image sample at
(t0,x0) to the true position (x,z) of the scatterer.
To find the apex position of the diffraction curve, I define
image rays for profile imaging to be the propagation paths of
the energy in the signals at the apex positions of diffraction curves
on a common shot gather. At the apex of a diffraction curve,
the derivative of the traveltime with respective to
the receiver location is zero.
Therefore, an image ray emerges vertically at the receiver location.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows an example of such an image ray.
By tracing the image ray passing through the scatterer
at subsurface position (x,z), we can find the coordinates
of the apex position of the diffraction curve, as follows:
shows an example of such an image ray.
By tracing the image ray passing through the scatterer
at subsurface position (x,z), we can find the coordinates
of the apex position of the diffraction curve, as follows:
| 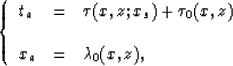 |
(5) |
where 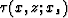 is the traveltime from shot location xs to
subsurface position (x,z), and
is the traveltime from shot location xs to
subsurface position (x,z), and 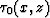 and
and 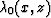 are the same as defined in equation (1).
Combining equations (5) and (3) gives
us the mapping functions of the time-to-depth conversion, as follows:
are the same as defined in equation (1).
Combining equations (5) and (3) gives
us the mapping functions of the time-to-depth conversion, as follows:
| ![\begin{displaymath}
\left\{
\begin{array}
{lll}
t_0 =\displaystyle{[\tau(x,z;x_s...
...x_s)+\tau_0(x,z)]} \\ \\ x_0 = \lambda_0(x,z)\end{array}\right.\end{displaymath}](img9.gif) |
(6) |
Once these two mapping functions are computed, the image-ray
corrections for profile imaging is again a variable-substitution process.





Next: Constant offset imaging
Up: GENERALIZED IMAGE-RAY METHOD
Previous: GENERALIZED IMAGE-RAY METHOD
Stanford Exploration Project
11/18/1997
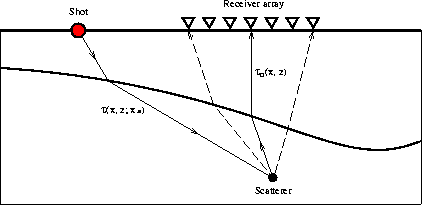
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the ray paths in a common shot experiment.
The seismic energy generated by a shot at surface location xs propagates
towards a point scatterer at subsurface position (x,z).
After being diffracted from the scatterer, the energy travels along the multiple
ray paths connecting the scatterer to each receiver of a receiver array.
On the recorded shot gather, the seismic
energy is distributed in the data samples along a diffraction curve
that is determined by the functional relationship between traveltime t and
receiver location xr. The diffraction curve has a hyperbolic shape
when the overburden velocities of the scatterer are free of lateral variations.
If we assume that the lateral velocity variations are confined
to a reasonable scale, this curve usually is well fit by a hyperbola
in the vicinity of its apex. Consequently, a profile time-migration
can collapse the energy distributed over this portion of the diffraction curve.
shows the ray paths in a common shot experiment.
The seismic energy generated by a shot at surface location xs propagates
towards a point scatterer at subsurface position (x,z).
After being diffracted from the scatterer, the energy travels along the multiple
ray paths connecting the scatterer to each receiver of a receiver array.
On the recorded shot gather, the seismic
energy is distributed in the data samples along a diffraction curve
that is determined by the functional relationship between traveltime t and
receiver location xr. The diffraction curve has a hyperbolic shape
when the overburden velocities of the scatterer are free of lateral variations.
If we assume that the lateral velocity variations are confined
to a reasonable scale, this curve usually is well fit by a hyperbola
in the vicinity of its apex. Consequently, a profile time-migration
can collapse the energy distributed over this portion of the diffraction curve.

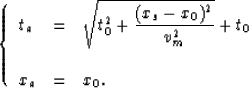
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows an example of such an image ray.
By tracing the image ray passing through the scatterer
at subsurface position (x,z), we can find the coordinates
of the apex position of the diffraction curve, as follows:
shows an example of such an image ray.
By tracing the image ray passing through the scatterer
at subsurface position (x,z), we can find the coordinates
of the apex position of the diffraction curve, as follows:
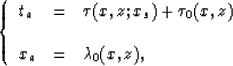
![\begin{displaymath}
\left\{
\begin{array}
{lll}
t_0 =\displaystyle{[\tau(x,z;x_s...
...x_s)+\tau_0(x,z)]} \\ \\ x_0 = \lambda_0(x,z)\end{array}\right.\end{displaymath}](img9.gif)