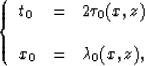
Before describing the image-ray method for prestack imaging, let me first review Hubral's image-ray concept for poststack imaging. On a stacked section, the energy diffracted from a point scatterer is distributed among signals upon its traveltime curve referred to as the diffraction curve. Although the diffraction curve becomes non-hyperbolic when overburden velocities of the scatterer vary laterally, it usually is well approximated by a hyperbola in the vicinity of its apex. Hence, the energy distributed over this portion of the curve can be focused around the apex position by time migration. To determine the depth-migrated position of the focused energy, Hubral (1977) introduced the concept of the image ray. According to his definition, image rays are the propagation paths of the energy in the signals at the apex positions of diffraction curves. Because diffraction curves have zero time-slope at their apex positions, all image rays shoot vertically at the surface. Suppose that an image ray connects surface point x0 and subsurface point (x,z), and that the two-way traveltime along this ray is t0. Then, the energy diffracted from a point scatterer at (x,z) is distributed along the diffraction curve whose apex is at (t0,x0). Consequently, if we assume that time migration focuses the energy along the diffraction curve onto the apex position of the curve, the mapping from (t0,x0) to (x,z) defines a general time-to-depth conversion for poststack imaging.
Let us suppose that we have a stacked section P(t,xr). If we depth-migrate this section, we would get the correct image Q(x,z). However, if we use a conventional time-migration to image this section, we obtain a time-migrated image P0(t0,x0). By tracing the image ray for each subsurface point (x,z), we can find two mapping functions of the time-to-depth conversion, as follow:
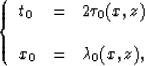 |
(1) |
| (2) |