Next: EXAMPLES
Up: ALGORITHM
Previous: Computation of traveltimes
To compute the amplitudes, we need to solve equations (14)
and (16). In polar coordinates, these two equations become:
| 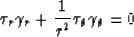 |
(24) |
and
| 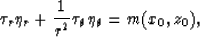 |
(25) |
respectively. Because the traveltimes are known now, these
two equations are first-order linear partial differential equations
in 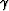 and
and  . The
algorithms for solving these two equations are very similar to the one for
traveltime calculation. To solve equation (24), we
replace equations (18) to (20) by
. The
algorithms for solving these two equations are very similar to the one for
traveltime calculation. To solve equation (24), we
replace equations (18) to (20) by
| 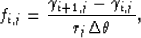 |
(26) |
| 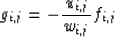 |
(27) |
and
| 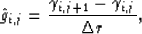 |
(28) |
respectively. As in the calculation of 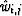 ,
the calculation of
,
the calculation of 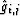 also involves four different cases:
also involves four different cases:
- 1.
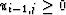 and
and 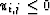
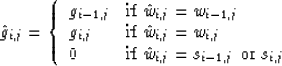
- 2.
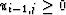 and ui,j > 0
and ui,j > 0
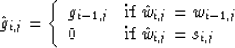
- 3.
- ui-1,j < 0 and
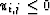
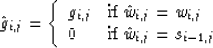
- 4.
- ui-1,j < 0 and ui,j > 0
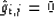
If 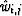 and
and 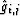 are calculated in one subroutine,
then the implementation is simple and the program is fully vectorizable,
which is shown as follows:
are calculated in one subroutine,
then the implementation is simple and the program is fully vectorizable,
which is shown as follows:
do i = 1,n+1
sign1 = 0.5*(1.+sign(1.,u(i-1)))
sign2 = 0.5*(1.+sign(1.,-u(i)))
hatw1 = sign1*min(w(i-1),s(i))+(1.-sign1)*s(i-1)
hatw2 = sign2*min(w(i),s(i-1))+(1.-sign2)*s(i)
hatw(i) = min(hatw1,hatw2)
sign3 = 0.5*(1.+sign(1.,w(i-1)-s(i)))
sign4 = 0.5*(1.+sign(1.,w(i)-s(i-1)))
sign5 = 0.5*(1.+sign(1.,hatw2-hatw1))
hatg1 = sign1*(1.-sign3)*g(i-1)
hatg2 = sign2*(1.-sign4)*g(i)
hatg(i) = sign5*hatg1+(1.-sign5)*hatg2
enddo
From equation (28), we have
| 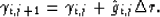 |
(29) |
I can apply Podvin and Lecomte's method to the computation of function
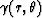 so that backward extrapolation can be handled.
so that backward extrapolation can be handled.
To solve equation (25), I use
![\begin{displaymath}
\eta_r = {1 \over \tau_r}[m(x_0,z_0)-{1 \over r^2}\tau_\theta\eta_\theta]\end{displaymath}](img63.gif)
to extrapolate the function 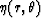 . Referring to the algorithm for
calculating
. Referring to the algorithm for
calculating 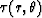 and
and 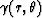 , one can
easily construct the algorithm for calculating function
, one can
easily construct the algorithm for calculating function 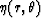 .
.
The Jacobian function in polar coordinates can be determined
from (13) as follows:
| 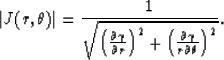 |
(30) |
We can either map this Jacobian function to Cartesian coordinates and
use equation (11) to calculate the amplitudes, or calculate the
amplitudes in polar coordinates and then map them to Cartesian
coordinates.





Next: EXAMPLES
Up: ALGORITHM
Previous: Computation of traveltimes
Stanford Exploration Project
12/18/1997
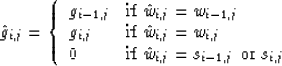
![]()
![]()
![]()
![]()