




Next: ALGORITHM
Up: THEORY
Previous: Traveltimes
Collecting the leading terms of amplitude in the ray series expansion
yields the zeroth order transport equation (Cervený et al., 1977):
| ![\begin{displaymath}
\nabla\tau\cdot\nabla A+{1 \over 2}\left[\nabla \ln \rho \cdot
\nabla \tau+ \nabla^2 \tau \right]A=0.\end{displaymath}](img18.gif) |
(10) |
If we assume that the traveltime function has been found by solving the
eikonal equation, then equation (10) is a first order,
linear partial differential equation (PDE). We see that
equation (10) contains the term 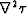 that is related to the derivatives of slowness function
with respect to the spatial
coordinates. Thus, the validity of this equation requires the slowness
function to be differentiable. If this requirement is met, we can
presumably solve this equation using a finite difference method.
An easier approach
(Cervený et al., 1977)
is to solve the transport equation in ray coordinates
and transform the analytical solution of the resulting
ODE to Cartesian coordinates, which yields
that is related to the derivatives of slowness function
with respect to the spatial
coordinates. Thus, the validity of this equation requires the slowness
function to be differentiable. If this requirement is met, we can
presumably solve this equation using a finite difference method.
An easier approach
(Cervený et al., 1977)
is to solve the transport equation in ray coordinates
and transform the analytical solution of the resulting
ODE to Cartesian coordinates, which yields
| 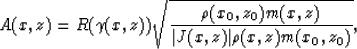 |
(11) |
where R is the radiation pattern of the source, 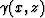 is the
take-off angle of the ray that reaches point (x,z), J(x,z) is the Jacobian
of the transformation from Cartesian coordinates to ray coordinates.
is the
take-off angle of the ray that reaches point (x,z), J(x,z) is the Jacobian
of the transformation from Cartesian coordinates to ray coordinates.
| 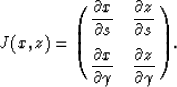 |
(12) |
In Appendix A, I show that for a 2-D medium and a line source
(the line source is aligned along the third dimension on which the slowness
does not depend),
| 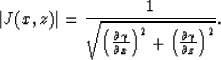 |
(13) |
Also in Appendix A,
I show that function 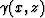 can be computed by solving
the first order linear PDE
can be computed by solving
the first order linear PDE
| 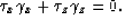 |
(14) |
with the initial condition that 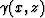 is equal to the take-off angle
at the source position.
is equal to the take-off angle
at the source position.
In seismic exploration, point sources may be more appropriate. Cerveny (1981)
shows that for point source, function J for line source should be multiplied
by a factor  to take account the geometric spreading in the third
dimension. He showed that
to take account the geometric spreading in the third
dimension. He showed that
| 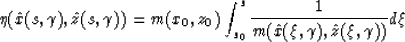 |
(15) |
where (x0,z0) is the coordinate of the source position.
I show, in Appendix B, that function 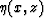 can be calculated
by solving a first order linear PDE:
can be calculated
by solving a first order linear PDE:
| 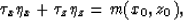 |
(16) |
The initial condition for solving equation (16)
is 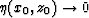 .The algorithm used for solving the eikonal equation, after some modifications,
can be used to solve PDEs (14) and (16).
It should be noted that all these formulas are valid only in a regular
region in which no caustics exist.
.The algorithm used for solving the eikonal equation, after some modifications,
can be used to solve PDEs (14) and (16).
It should be noted that all these formulas are valid only in a regular
region in which no caustics exist.





Next: ALGORITHM
Up: THEORY
Previous: Traveltimes
Stanford Exploration Project
12/18/1997
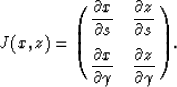
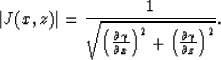
![]() to take account the geometric spreading in the third
dimension. He showed that
to take account the geometric spreading in the third
dimension. He showed that