




Next: Traveltimes
Up: Zhang: F-D calculation
Previous: Introduction
The elastic wave equation for an isotropic, 2-dimensional
medium has a well-known form:
| ![\begin{displaymath}
\begin{array}
{lll}
\rho \displaystyle{\partial^2 u_1 \over ...
...displaystyle{\partial u_1 \over \partial z})\right],\end{array}\end{displaymath}](img1.gif) |
(1) |
where u1 and u2 are the x- and z-components of
the displacement vector,
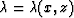 and
and 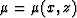 are the
elastic constants of the media, and
are the
elastic constants of the media, and 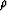 is the density of the medium.
Using asymptotic ray theory, we can expand the Green's function of
this wave equation into a ray series
at high frequencies (Cervený et al., 1977).
The leading term of this ray series has two components:
GP for the compressional wave (P-wave) and GS for the shear wave (S-wave):
is the density of the medium.
Using asymptotic ray theory, we can expand the Green's function of
this wave equation into a ray series
at high frequencies (Cervený et al., 1977).
The leading term of this ray series has two components:
GP for the compressional wave (P-wave) and GS for the shear wave (S-wave):
| 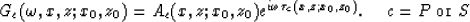 |
(2) |
In this equation, 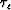 is the traveltime it takes for a wave to propagate
from a source location (x0,z0) to an observation location (x,z).
The traveltime function satisfies the eikonal equation of wave equation
(1). If we assume that the medium is smoothly varying,
then function Ac
describes the amplitude decay of this propagation due to geometric spreading,
and it satisfies the first order transport equation. Because the
Green's functions for P-wave and S-wave have a common form,
from now on, we drop the subscripts P
and S, and make distinctions only when necessary.
is the traveltime it takes for a wave to propagate
from a source location (x0,z0) to an observation location (x,z).
The traveltime function satisfies the eikonal equation of wave equation
(1). If we assume that the medium is smoothly varying,
then function Ac
describes the amplitude decay of this propagation due to geometric spreading,
and it satisfies the first order transport equation. Because the
Green's functions for P-wave and S-wave have a common form,
from now on, we drop the subscripts P
and S, and make distinctions only when necessary.





Next: Traveltimes
Up: Zhang: F-D calculation
Previous: Introduction
Stanford Exploration Project
12/18/1997
![\begin{displaymath}
\begin{array}
{lll}
\rho \displaystyle{\partial^2 u_1 \over ...
...displaystyle{\partial u_1 \over \partial z})\right],\end{array}\end{displaymath}](img1.gif)
![\begin{displaymath}
\begin{array}
{lll}
\rho \displaystyle{\partial^2 u_1 \over ...
...displaystyle{\partial u_1 \over \partial z})\right],\end{array}\end{displaymath}](img1.gif)