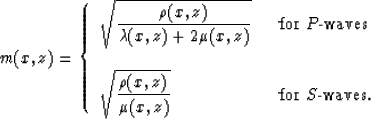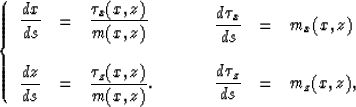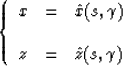Next: Amplitudes
Up: THEORY
Previous: THEORY
The eikonal equation in two dimensions relates the two gradient components
of the traveltime field as follows:
| 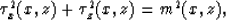 |
(3) |
where subscripts x and z denote partial derivatives with respect to x
and z, respectively, and m(x,z) is the slowness model of the medium
determined by
| 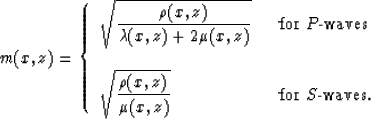 |
(4) |
Traditionally, the eikonal equation is solved by using the method of
characteristics. The characteristic curves of this equation are rays
described by the ray equations
| 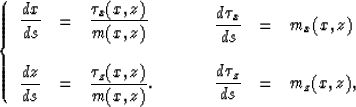 |
(5) |
where variable s is the arc-length of the ray.
The solutions to the ray equation define a transformation between the
coordinate system (x,z) and a new coordinate system 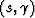 , named
ray coordinates, as follows:
, named
ray coordinates, as follows:
| 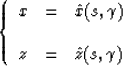 |
(6) |
For each fixed 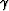 , this pair of equations give the Cartesian coordinates
of a ray. The variations of
, this pair of equations give the Cartesian coordinates
of a ray. The variations of 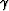 span a set
of rays covering the whole (x,z) space. If we substitute (x,z) in
equation (6) into the eikonal equation, we obtain an ordinary
differential equation (ODE) along each ray:
span a set
of rays covering the whole (x,z) space. If we substitute (x,z) in
equation (6) into the eikonal equation, we obtain an ordinary
differential equation (ODE) along each ray:
| 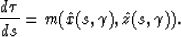 |
(7) |
The solution of this ODE is simply an integral along the ray:
| 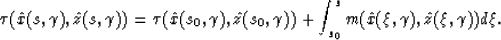 |
(8) |
This traveltime calculation method is called ray tracing method.
The ray tracing method computes traveltimes along rays, hence
generates a traveltime map on an irregular grid.
Many seismic modeling and imaging algorithms require a traveltime map
on a regular grid. An efficient way to obtain this traveltime map is to solve
the eikonal equation directly using a finite difference scheme. The finite
difference calculation of traveltimes is actually an extrapolation process.
The traveltime function is locally extrapolated from the grid points where the
traveltimes are known to their neighboring grid points where the
traveltimes are unknown by following the principle that the gradients of
the traveltimes satisfy the eikonal equation.
This process starts from the source position where the traveltime is zero,
and is repeated until all grid points are filled. We can also
extrapolate the gradients of traveltimes.
The gradients of traveltimes are vectors and have two components in
two dimensions. In order to determine both components, we need one more
equation besides the eikonal equation. Van Trier and Symes (1990)
use the following one:
| 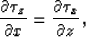 |
(9) |
where 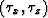 are the two components of the traveltime gradient.
Van Trier and Symes interpret this equation using the flux conservation
principle. If we rewrite equation (9) as
are the two components of the traveltime gradient.
Van Trier and Symes interpret this equation using the flux conservation
principle. If we rewrite equation (9) as
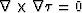 , we see
that this equation states that a gradient field is curl-free.
Once the traveltime gradients are computed, their integrations give
the traveltimes.
, we see
that this equation states that a gradient field is curl-free.
Once the traveltime gradients are computed, their integrations give
the traveltimes.





Next: Amplitudes
Up: THEORY
Previous: THEORY
Stanford Exploration Project
12/18/1997