




Next: THE EQUIVALENT HOMOGENEOUS MEDIUM
Up: EVALUATION OF VOLUME INTEGRALS
Previous: Field discontinuities
As before, we are free to rewrite the above integral relationships
in a form which incorporates the boundary conditions occurring at a
material discontinuity surface:
| 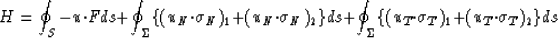 |
(9) |
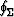 stands for an integral over all points in the medium which
exhibit material and thus stress and strain discontinuities.
uN and uT are displacements at the discontinuity interface, generated
by the normal and tangential strains in effect on an infinitesimal
surface element.
For convenience we look at a small piece of such a discontinuity surface. The symbol < > means the addition of the two opposite surface effects.
At a small surface region
stands for an integral over all points in the medium which
exhibit material and thus stress and strain discontinuities.
uN and uT are displacements at the discontinuity interface, generated
by the normal and tangential strains in effect on an infinitesimal
surface element.
For convenience we look at a small piece of such a discontinuity surface. The symbol < > means the addition of the two opposite surface effects.
At a small surface region 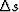 , we obtain then
, we obtain then
| 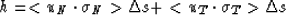 |
(10) |
Since the boundary conditions on welded interfaces require that 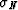 and
u (
and
u (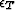 ) are continuous we can write for the change in surface energy:
) are continuous we can write for the change in surface energy:
| 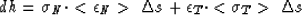 |
(11) |
We note that only the discontinuous components are in < > .
Expressing these discontinuous components in terms of continuous ones
using the constitutive equation
| 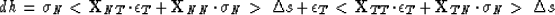 |
(12) |
Separating out the continuous quantities and rewriting it as a matrix
equation gives:
| 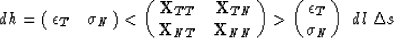 |
(13) |
This takes care of one boundary point. Choosing an infinitesimal
boundary region ds we can integrate the above expression over all
discontinuity surfaces within the volume
| 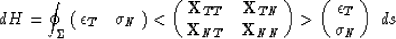 |
(14) |
Consequently we obtain the elastic energy stored by deforming the medium. Note
that this expression is an exact formula for calculating the energy; however
all the quantities including the stresses and strains at each point inside
the medium must be known.
If we are willing to sacrifice exactness, we can approximate H by assuming
an average stress and strain in the medium. Then the composite medium property
depends only on properties of its composites by:
| 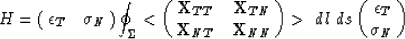 |
(15) |
It is remarkable that in the layered geometry (14) and (15)
are identical and thus exact. For an arbitrary heterogeneous medium
the scale of heterogeneity determines the accuracy of approximation (15)
to (14). The stress and strain field in the medium is not
distorted much by small scale heterogeneities. Thus on an average much
larger than the scale of the heterogeneities the stress and strain field
is assumed to be constant, so that we can apply relation (15).





Next: THE EQUIVALENT HOMOGENEOUS MEDIUM
Up: EVALUATION OF VOLUME INTEGRALS
Previous: Field discontinuities
Stanford Exploration Project
1/13/1998