




Next: Field discontinuities
Up: Karrenbach: Equivalent Medium
Previous: INTERIOR BOUNDARY CONDITIONS
Above we have formally defined the equations which govern the averaging
process (2,3 and 5). Instead of calculating the
volume integral, the problem can be transformed into an evaluation of
surface integrals.
Greens Theorem is valid for tensors of any order. In its most general form
it is written as
| 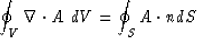 |
(6) |
A can be a vector, then 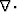 is the divergence operator and the
theorem is termed ``Gauss' Theorem'';
or A can be a tensor, with the appropriate definition for
is the divergence operator and the
theorem is termed ``Gauss' Theorem'';
or A can be a tensor, with the appropriate definition for 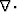 .
.





Next: Field discontinuities
Up: Karrenbach: Equivalent Medium
Previous: INTERIOR BOUNDARY CONDITIONS
Stanford Exploration Project
1/13/1998