




Next: Energy at a discontinuity
Up: EVALUATION OF VOLUME INTEGRALS
Previous: EVALUATION OF VOLUME INTEGRALS
If a volume contains an arbitrary surface  across
which A is discontinuous, then
application of Greens Theorem to the subvolumes, Figure
across
which A is discontinuous, then
application of Greens Theorem to the subvolumes, Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) turns a
volume integral in a sum of surface integrals.
turns a
volume integral in a sum of surface integrals.
| 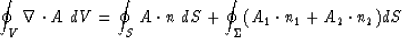 |
(7) |
n1 and n2 are the unit normals when approaching the discontinuity
surface either from side 1 or the side 2. A1 and A2 are forces on opposite sides of the surface.
The first term is the integral over the exterior surface, while the second
term accounts for effects created by interior discontinuity surfaces.
Applying the Greens Theorem (6) to the energy integral 5,
which we want to calculate, we get:
| 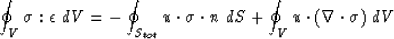 |
(8) |
where 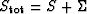 is the sum of exterior and interior surfaces.
In the static case the divergence of the stress
is the sum of exterior and interior surfaces.
In the static case the divergence of the stress 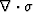 at any point in the medium is zero.
If it were not zero we would have a net force acting
on some part of the medium; then the medium would not be in equilibrium
and would accelerate according to Newton's law
(
at any point in the medium is zero.
If it were not zero we would have a net force acting
on some part of the medium; then the medium would not be in equilibrium
and would accelerate according to Newton's law
(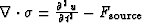 ).
This static argument is equivalent to saying: after an external force is
applied to the medium, we wait for a long time until
the medium is in equilibrium
(or there is no energy any more in form of elastic waves traveling
though the medium).
).
This static argument is equivalent to saying: after an external force is
applied to the medium, we wait for a long time until
the medium is in equilibrium
(or there is no energy any more in form of elastic waves traveling
though the medium).





Next: Energy at a discontinuity
Up: EVALUATION OF VOLUME INTEGRALS
Previous: EVALUATION OF VOLUME INTEGRALS
Stanford Exploration Project
1/13/1998
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) turns a
volume integral in a sum of surface integrals.
turns a
volume integral in a sum of surface integrals.
![]() across
which A is discontinuous, then
application of Greens Theorem to the subvolumes, Figure
across
which A is discontinuous, then
application of Greens Theorem to the subvolumes, Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) turns a
volume integral in a sum of surface integrals.
turns a
volume integral in a sum of surface integrals.