




Next: INTERIOR BOUNDARY CONDITIONS
Up: Karrenbach: Equivalent Medium
Previous: Introduction
Three basic conservation laws govern the behavior of an inhomogeneous
anisotropic medium and its equivalent homogeneous counterpart.
An arbitrary region V in three dimensions is shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . The region is bounded by surface S.
The quantities we want to preserve in our equivalent medium are:
total energy change, total volume change and total mass.
. The region is bounded by surface S.
The quantities we want to preserve in our equivalent medium are:
total energy change, total volume change and total mass.
The volume, shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , changes its shape in response to the
application of some external force on its exterior surface.
The total energy during this process is the sum of the elastically
stored energy in volume V, the total surface energy on boundary S,
the kinetic energy and the energy provided
by sources within the medium:
, changes its shape in response to the
application of some external force on its exterior surface.
The total energy during this process is the sum of the elastically
stored energy in volume V, the total surface energy on boundary S,
the kinetic energy and the energy provided
by sources within the medium:
| 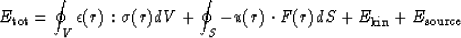 |
(1) |
where u the displacement vector and F is the vector
of force applied to the exterior surface S.
The contribution of energy in response to a force acting on the exterior of the medium
is calculated by the dot product of displacement and force integrated over the
whole exterior surface.
The material has a stiffness that may depend on spatial variables.
The strain 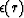 in the medium is proportional
to the stress
in the medium is proportional
to the stress 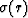 present.
So part of the energy is elastically stored in the medium. It can be calculated
by taking the double dot product of stress and strain
and integrating it over the whole volume.
In the static
case we neglect kinetic energy
present.
So part of the energy is elastically stored in the medium. It can be calculated
by taking the double dot product of stress and strain
and integrating it over the whole volume.
In the static
case we neglect kinetic energy 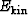 , which is equivalent to
waiting until the medium reaches a state of equilibrium.
Omitting the
, which is equivalent to
waiting until the medium reaches a state of equilibrium.
Omitting the 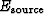 term implies having no elastic sources
within the medium.
The total volume change
term implies having no elastic sources
within the medium.
The total volume change 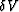 in response to an application of an external force is
in response to an application of an external force is
| 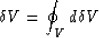 |
(2) |
The total mass m of the medium after deformation is
| 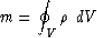 |
(3) |
The equivalent homogeneous medium should have the following
desired properties. There should be no change in the total mass. The total
volume change should be identical to the homogeneous medium. When external
forces are applied, the change in the sum of surface and deformation energy
should be the same for the homogeneous and heterogeneous medium.
On interior boundaries we want welded contacts; internal
interfaces are not allowed to slip. This specification is important,
since it governs the later choice of boundary decomposition.





Next: INTERIOR BOUNDARY CONDITIONS
Up: Karrenbach: Equivalent Medium
Previous: Introduction
Stanford Exploration Project
1/13/1998
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . The region is bounded by surface S.
The quantities we want to preserve in our equivalent medium are:
total energy change, total volume change and total mass.
. The region is bounded by surface S.
The quantities we want to preserve in our equivalent medium are:
total energy change, total volume change and total mass.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . The region is bounded by surface S.
The quantities we want to preserve in our equivalent medium are:
total energy change, total volume change and total mass.
. The region is bounded by surface S.
The quantities we want to preserve in our equivalent medium are:
total energy change, total volume change and total mass.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , changes its shape in response to the
application of some external force on its exterior surface.
The total energy during this process is the sum of the elastically
stored energy in volume V, the total surface energy on boundary S,
the kinetic energy and the energy provided
by sources within the medium:
, changes its shape in response to the
application of some external force on its exterior surface.
The total energy during this process is the sum of the elastically
stored energy in volume V, the total surface energy on boundary S,
the kinetic energy and the energy provided
by sources within the medium: