15: COMPARISON OF PRE- AND POST-STACK MIGRATION

For any single fold gather

$$s=\Phi _{I}(\lambda ), {\:}r=\Psi _{I}(\lambda )$$

there is only one family of stacking lines forming the IG-operator which transforms the field $u_{0}(s(\lambda ),r(\lambda ), t)$ into the depth migration section (2D case) or volume (3D case). This operator has a structure ${\bf P}_{w}{\bf D}_{(-)}^{k}$ where w is a weight function that may satisfy some additional condition, $k={(n-1) \over 2}$, where n is the dimension of the problem. But when we have a multi-fold observational system there are different ways to perform depth migration. Any continuous system of observations may be considered as a family of basic gathers  

$$s=\Phi _{\alpha }(\lambda ), {\:}r=\Psi _{\alpha }(\lambda )$$ (137)

where $\alpha$ is a continuous parameter. The choice of a basic gather determines parametrization of a multi-fold observational system. If, for instance, basic gather is a common offset pattern, then

$$s=X-h, {\:}r=X+h$$

where h plays the role of $\alpha$ and X plays the role of $\lambda$. Exchanging roles of X and h gives common-mid-point parametrization. If we consider multi-fold systems as a family of common source patterns, then $\alpha =s$ and $r=s+\lambda$ and so on.

For any such description of the observational system, we define prestack migration as  

$$M_{I}(x,z)=\int M(x,z,\alpha )d\alpha$$ (138)

where  

$$M(x,z,\alpha )={\bf P}_{w}^{\lambda }{\bf D}_{(-)}^{k}u_{0}(\lambda ,\alpha ,t)$$ (139)

and

$$u_{0}(\lambda ,\alpha ,t)=u_{0}(\Phi _{\alpha }(\lambda ), \Psi _{\alpha }(\lambda ),t)$$

The operator ${\bf P}_{w}^{\lambda }$ in equation (140) acts on variable $\lambda$ and has the following stacking lines:

$$\theta _{\alpha } (\lambda,x,z)=T(\Phi _{\alpha }(\lambda ), x,z) + T (\Psi _{\alpha } (\lambda ),x,z).$$

We may shortly describe this scheme by the symbol sequence $\sum _{\alpha } {\bf P}_{w}^{\lambda }{\bf D}_{(-)}^{m}$, where $\sum _{\alpha }$ is the operator of simple stacking (without time or depth shifts).

It is natural to consider r and s as primary coordinates of observations. Then any other description of equation (137) is a change of the system of coordinates. In order to stress this, we can rewrite equation (137) in the form

$$s=\Phi (\lambda ,\alpha ),{\:}r=\Psi (\lambda , \alpha ).$$

If w_s(x,z,r) is a weight function of the operator ${\bf P}_{w_{s}}^{r}$ transforming common-shot-point records to a depth migrated section (volume) and we choose:

$$w_{\alpha }(x,z,\lambda )= {D(s,r)\over D(\lambda ,\alpha )}w_{\Phi _{\alpha }(\lambda)} (x,z, \Psi _{\alpha }(\lambda ))$$

then

$$\Sigma_{\alpha }{\bf P}^{\lambda }_{w_{\alpha }}u_{0}(\lambda ,\alpha ,t) =\Sigma _{s}{\bf P}^{r}_{w_{s}}u_{0}(s,r,t).$$

More fully, it is:

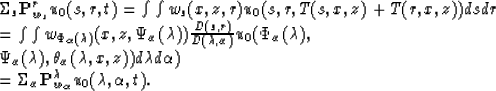The proved relation means that under a proper choice of weight function, migration does not depend on the choice of a basic data pattern. Of course, this statement does not take into account some practical aspects that can be connected with numerical realizations of operators ${\bf P}^{\lambda }_{w_{\alpha }}$ and ${\bf P}^{r}_{w_{s}}$.

A particular case of the scheme  (138)-(139) is the situation where the operator ${\bf P}^{\lambda }_{w_{\alpha }}$ is split into the sequence of two or more operators. For example, when

$${\bf P}^{\lambda }_ {w_{\alpha }}={\bf P}^{x}_{w_{0}}{\bf Q}^{\lambda }_{\hat{w}_{\alpha }}$$

where ${\bf P}^{x}_{w_{0}}$ realizes transformation of zero offset time section into the depth migrated section and ${\bf Q}^{\lambda }_{\hat{w}_{\alpha }}$ is IG-operator that transform basic gather into the zero offset time section. Let the basic pattern be a common-offset gather. Then the operator ${\bf Q}^{\lambda }_{\hat{w}_{\alpha }}$may be represented in a form

$${\bf Q}^{\lambda }_{\hat{w}_{\alpha }} =DMO \cdot NMO$$

But this representation determines the same prestacking migration. It means that without the loss of generality, we can restrict ourselves by consideration of the operator $\sum_{s}{\bf P}^{r}_{w_{s}}{\bf D}^{k}_{(-)}$, having chosen common-source gather as a basic pattern.

In principle, another way to provide depth migration is the routine scheme (post-stack migration):

$$M_{\Pi }(x,z)={\bf P}_{w_{0}}^{x}{\bf D}^{k}_{(-)}\sum_{h}\cdot NMO u_{0}(h,x,t)$$

(where $x={(r+s)\over 2} {\:}h={(r-s)\over 2}$). The operator sequence $\sum_{h} \cdot NMO$ describes common-midpoint stacking.

Geophysicists know advantages and disadvantages of both schemes. It is known, for example, that post-stack migration is a rather robust procedure with respect to a prior knowledge of velocity model, but it fails when the velocity model is complicated. On the other hand, prestack migration needs good information about the velocity distribution in the subsurface. But once we have this information we can perform correct imaging even in rather complicated situations.

Is it possible to connect this judgment with some quantitative characteristics? Let us denote q as an order of discontinuity in primary wave field u₀ (s,r,t) and q^' an order of discontinuity after migration. We remind the reader that a discontinuity is a model of reflected wave.