




Next: 15: COMPARISON OF PRE-
Up: 12: OPERATOR OF INTEGRAL
Previous: Dynamics of the main
Integral (126) describes the situation in the linear tomography when
rays can be parametricized as a function of 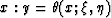 and
and
| 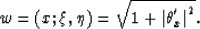 |
(129) |
The general problem of tomography is the reconstruction of the field u0(x,y)
using the given field 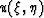 . We shall reduce this problem to a
simpler one: to reconstruct the discontinuities of the field u0(x,y). The
possibility of this reduction follows from the fact that discontinuities are
a model for the most vivid particularities of the object.
. We shall reduce this problem to a
simpler one: to reconstruct the discontinuities of the field u0(x,y). The
possibility of this reduction follows from the fact that discontinuities are
a model for the most vivid particularities of the object.
So our task is to find such an operator  , that
, that
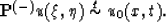
Let us introduce a dual IG-operator
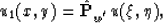
which has the family of dual lines 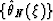 as a system
of stacking lines and an arbitrary kernel w'=w'(M,N).
It follows from the results of Chapter 12 that for any kernel w', the
operator
as a system
of stacking lines and an arbitrary kernel w'=w'(M,N).
It follows from the results of Chapter 12 that for any kernel w', the
operator 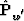 gives geometrical reconstruction of the original
discontinuity of the field u0(x,y) since this operator realizes the mapping
gives geometrical reconstruction of the original
discontinuity of the field u0(x,y) since this operator realizes the mapping
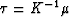 .It is clear that the operator
.It is clear that the operator 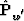 transforms the dynamics of a discontinuity of the field
transforms the dynamics of a discontinuity of the field 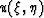 in the
same way as the operator
in the
same way as the operator 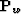 did. Then, according to formula (126)
did. Then, according to formula (126)
| ![\begin{displaymath}
U_{1} \sim \hat{{\bf P}}_{w^{'}} u \sim \kappa^{'} {\left[ \...
...A^{'} \right] }_{\omega}R^{(+)}_{q^{''},
\nu ^{''}}[y-\tau (x)]\end{displaymath}](img785.gif) |
(130) |
where 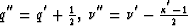
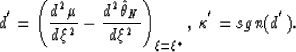
We have taken into account that
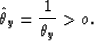
Now, combining formulae (128) and (130), we have:
![\begin{displaymath}
u_{1}(x,y) \sim \kappa \kappa^{'} { \left[ \sqrt{{2\pi \over...
...0} \right] }_{{\omega}} R^{(+)}_{q^{''},\nu ^{''}}
[y-\tau (x)]\end{displaymath}](img789.gif)
where
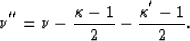
The operator 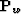 acts like
acts like
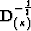 and the operator
and the operator 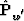 acts like
acts like
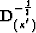 .
This means that in order to reconstruct the
order and the index of discontinuities we shall apply the correction filter
.
This means that in order to reconstruct the
order and the index of discontinuities we shall apply the correction filter
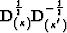 .
It can be shown that independently
on the curve
.
It can be shown that independently
on the curve 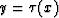
| 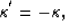 |
(132) |
consequently, the correction filter is
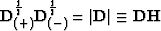 . It follows from equations (131)
and (132) that
. It follows from equations (131)
and (132) that
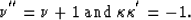
But
![\begin{displaymath}
{\bf D}{\bf H}[-R_{q+1,\nu +1}] \sim -R_{q,\nu +2} \sim - {\bf{H}}^{2}R_{q,\nu }
\sim R_{q,\nu}\end{displaymath}](img797.gif)
since 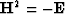 .
.
The kernal w' must be chosen from the condition
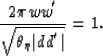
I have proven that
dd'=FG
where
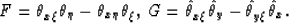
Consequently,
| 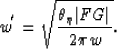 |
(133) |
So we have shown that
| 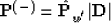 |
(134) |
where w' is expressed by Formula (133).
For example, let
| 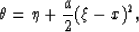 |
(135) |
then
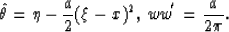
If equation (135) is an equation of rays in ray tomography, then according
to equation (129)
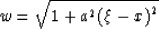
and
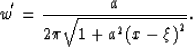
Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) -
-![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) give an illustration of reconstruction of the
step-function
give an illustration of reconstruction of the
step-function
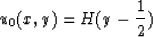
given at the square  (equation (126)).
Figure
(equation (126)).
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) a shows the field
a shows the field 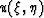 . Figure
. Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) b is a result of application
of the simplest operator
b is a result of application
of the simplest operator 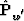 at
at 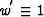 .
Figure
.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) c
is a result of application of the operator
c
is a result of application of the operator 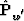 with w'
chosen according to equation(135), And Figure
with w'
chosen according to equation(135), And Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) d gives the field
d gives the field
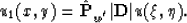
It is interesting that Kirchhoff's operators of the forward and reverse
wave-field continuation originate a symmetrical pair of asymptotically inverse operators
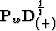 and
and 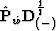 with
with
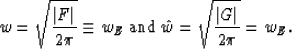
In the n-dimensional case we have the following analog of formula (134)
| 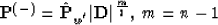 |
(136) |
where the kernel w' is expressed by the same formula (133) but F and
G are determinants of the correspondent matrices.
The formula (111) and (113) were published first by Gr. Beylkin (1984)
who applied a very different approach connected with the theory
of pseudodifferential operators.





Next: 15: COMPARISON OF PRE-
Up: 12: OPERATOR OF INTEGRAL
Previous: Dynamics of the main
Stanford Exploration Project
1/13/1998
![]() and
and
![]() , that
, that
![]()
![]()
![\begin{displaymath}
U_{1} \sim \hat{{\bf P}}_{w^{'}} u \sim \kappa^{'} {\left[ \...
...A^{'} \right] }_{\omega}R^{(+)}_{q^{''},
\nu ^{''}}[y-\tau (x)]\end{displaymath}](img785.gif)
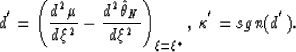
![]()
![\begin{displaymath}
u_{1}(x,y) \sim \kappa \kappa^{'} { \left[ \sqrt{{2\pi \over...
...0} \right] }_{{\omega}} R^{(+)}_{q^{''},\nu ^{''}}
[y-\tau (x)]\end{displaymath}](img789.gif)
![]()
![]() acts like
acts like
![]() and the operator
and the operator ![]() acts like
acts like
![]() .
This means that in order to reconstruct the
order and the index of discontinuities we shall apply the correction filter
.
This means that in order to reconstruct the
order and the index of discontinuities we shall apply the correction filter
![]() .
It can be shown that independently
on the curve
.
It can be shown that independently
on the curve ![]()
![]()
![]()
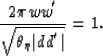
![]()
![]()
![]()
![]()
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) -
-![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) give an illustration of reconstruction of the
step-function
give an illustration of reconstruction of the
step-function
![]()
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) a shows the field
a shows the field ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) b is a result of application
of the simplest operator
b is a result of application
of the simplest operator ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) c
is a result of application of the operator
c
is a result of application of the operator ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) d gives the field
d gives the field
![]()
![]() and
and ![]() with
with
![]()