




Next: Application to tomography
Up: 12: OPERATOR OF INTEGRAL
Previous: Geometry of the main
Our task is to describe the profile of the main discontinuity of the field
| 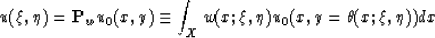 |
(126) |
along the line 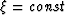 .I remind you that
.I remind you that
![\begin{displaymath}
u_{0}(x,y)\stackrel{q}{\sim }A_{0}(x)R^{(+)}_{q,\nu }[y-\tau (x)].\end{displaymath}](img763.gif)
Applying the operator 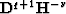 we obtain the field
we obtain the field
![\begin{displaymath}
U(\xi ,\eta ) \sim \int w(x;\xi , \eta ){\vert\th _{\eta }\vert}^{q+1}A_{0}(x)\delta
[
\th _{M}(x)-\tau (x)]dx.\end{displaymath}](img765.gif)
Then we fix a line in the plane 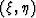 :
:
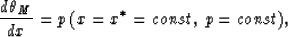
which we shall call a pseudoray. For each point M' belonging to the
pseudoray, we apply the expansion of the difference
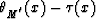 into Taylor's series in a neighborhood of the point
into Taylor's series in a neighborhood of the point
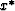 :
:
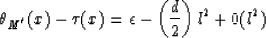
where 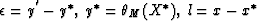 and
and
![\begin{displaymath}
d={ \left[ {d^{2}\tau \over dx^{2}}-{d^{2}\th _{M} \over dx^{2}} \right]}_{x=
x^{\ast }}.\end{displaymath}](img771.gif)
The above equations are absolutely the same as those that we have already done
for the KO. As a result, we will receive a very similar formula
describing the field U(M'):
| ![\begin{displaymath}
U(M^{'}) \sim {\left[ \sqrt{{2\pi \over \vert d\vert}} {\ver...
...0}
\right] }_{{\omega}}R^{(\kappa )}_{-{1 \over 2}} (\epsilon )\end{displaymath}](img772.gif) |
(127) |
where 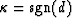 .
.
But here we have some important differences that we have to take into account:
Formula (127) describes the profile of the discontinuity along the
pseudoray but not along a line 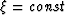 . There is a formalism that connects
different profiles of discontinuity. I shall omit this consideration and give
you only the final result under
. There is a formalism that connects
different profiles of discontinuity. I shall omit this consideration and give
you only the final result under 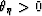 :
:
| ![\begin{displaymath}
u(\xi ,\eta )\stackrel{q^{'}}{\sim }{({\bf D}^{q+1}{\bf H}^{...
...wA_{0} \right] }_{{\omega}}R^{(+)}_{q^{'},\nu ^{'}}[y-\tau (x)]\end{displaymath}](img775.gif) |
(128) |
where 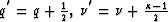 .I consider this formula to be the main result of the developing theory.
.I consider this formula to be the main result of the developing theory.





Next: Application to tomography
Up: 12: OPERATOR OF INTEGRAL
Previous: Geometry of the main
Stanford Exploration Project
1/13/1998
![]()
![]()
![]()
![]()
![]()
![\begin{displaymath}
U(M^{'}) \sim {\left[ \sqrt{{2\pi \over \vert d\vert}} {\ver...
...0}
\right] }_{{\omega}}R^{(\kappa )}_{-{1 \over 2}} (\epsilon )\end{displaymath}](img772.gif)
![]() . There is a formalism that connects
different profiles of discontinuity. I shall omit this consideration and give
you only the final result under
. There is a formalism that connects
different profiles of discontinuity. I shall omit this consideration and give
you only the final result under ![]() :
:
![\begin{displaymath}
u(\xi ,\eta )\stackrel{q^{'}}{\sim }{({\bf D}^{q+1}{\bf H}^{...
...wA_{0} \right] }_{{\omega}}R^{(+)}_{q^{'},\nu ^{'}}[y-\tau (x)]\end{displaymath}](img775.gif)