Post-stack migration

The operator $\sum_{h} \cdot NMO(v_{st})$ supplies the order $r=\infty$ only in the situation when mid-point travel-time curve is a hyperbola (as stacking lines). This is possible only for the simplest model of planar reflectors, and for the stacking velocity

$$v_{st}={v\over \cos \phi}.$$

In this case $q^{'}_{\Pi }=q$.

Let's examine a more complicated media. In any situation there is an optimal value v_opt of stacking velocity that supplies the order of touching $r\geq 3$.Let us put  

$$v_{st}={1\over \sqrt{vt_{0}t^{''}}}$$ (141)

where

$$t_{0}=t_{X}(0), {\:}t^{''}={d^{2}t_{X}\over dh^{2}},$$

t_X(h) - common-mid-point travel-time function.

One can easily check that condition (141) supplies the order of touching r=2. But both stacking hyperbola or common-mid-point travel-time curve are even functions (with respect to h) so third derivatives of both functions at h=0 are equal to . It means that r=3 and

$$q^{'}_{II}=q+{1\over 4}$$

We shall give some examples of optimal stacking velocities:

• if v(x,z) is constant and reflector is curved, then

  $$v_{opt}={v\over \cos \phi }$$

  where $\phi$ is a slope of the reflector at the base of the normal ray from the point X.
• If v(x,z)=v(z) and $\phi = 0$, then

  $$v_{opt}=v_{rms}={\left( 2t^{-1}_{0}\int^{H}_{0} v(z)dz\right) }^{{1\over 2}}$$

  (H is the reflector's depth).
• If v(x,z)=v(t) and a reflector is curved, then

  $$v_{opt}={ \left( {\int^{H}_{0}{v(z)dt\over {[1-p^{2}v^{2}(z)... ...{0}{dz\over v(z)\sqrt{1-p^{2}v^{2}(z)}}} \right) }^{{1\over 2}}$$

  where $p=v^{-1}(H)\sin \phi$.

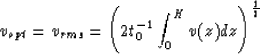
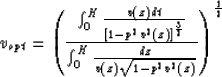
In practice, the optimal value of extreme velocity can be achieved as a result of velocity spectra analysis.

So, we have

$$q\leq q^{'}_{II} \leq q+{1\over 4}.$$

Accurate optimization of migration velocity for prestack migration is also possible. Let us consider the example of a flat horizontal reflector in vertically inhomogeneous velocity v=v(z). It can be shown that at v_m=v_rms the second derivative of the function z=h(x) which describes the shape of the reflector's image equals to (under x=s). The function h(x) is symmetrical with respect to the point x=s and it means that again r=3 and $q^{'}_{I}=q+{1\over 4}$.

It is interesting to note that the operator $\sum _{s}{\bf P}^{r}_{w_{s}}(v_{rms}) {\bf D}^{k}_{(-)}$ gives the good order $q+{1\over 4}$ but wrong depth $H^{'}= {1\over 2}t_{0}v_{rms}\neq H={1\over 2}t_{0}\bar{v}$ ($\bar{v}$ is an average velocity). On the other hand, the operator $\sum_{s}{\bf P}^{r}_{w_{s}}(\bar{v}){\bf D}^{k} _{(-)}$ gives the order $q+{1\over 2}$ but the correct depth H^'=H.

To perform post-stack migration for this model we can use the operator
${\bf P}_{w_{0}}({v}){\bf D}^{k}_{(-)}\sum_{h}NMO(v_{rms})$ which simultaneously gives $q^{'}=q+{1\over 4}$ and H^'=H.

When there is no symmetry in the medium, optimal migration velocity in prestack migration guarantees only r=2. So in general,

$$q\leq q^{'}_{I}\leq q+{1\over 3}$$

It is necessary to remember that q^'_II=q is possible only for the simplest model of medium. Prestack migration can be used in more complicated situations, provided there is enough knowledge of the velocity model. But when the velocity model is not well known then post-stack velocity is more robust. It is necessary to add that estimation of optimal stacking velocities needs less computer time then estimation of optimal migration velocities. But, at the same time, optimal stacking velocities enable us to obtain the correct velocity model. So, in complicated situations, it is necessary to use both schemes in a definite order.