




Next: 9: INTEGRAL OPERATORS OF
Up: 8: CLASSIFICATION OF K-OPERATORS
Previous: Differential K-operators
Let us consider the equation:
| 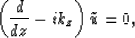 |
(95) |
at
kz=kz(z).
For homogeneous medium this equation can be obtained by splitting the wave
equation operator 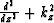 . Equation (95)
has the solution:
. Equation (95)
has the solution:
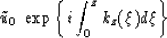
which describes upgoing waves.
The operator
| 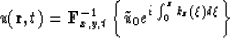 |
(96) |
is kinematically equivalent (in the sense of the classical eikonal equation), but
there is no partial derivative equation in space-time domain that has equation (96)
as a solution. This operator is an example of PDKO (Pseudo-Differential
K-Operator).
But we can find a sequence of equations
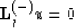
for which:
- each equation permits only one-way propagation along the z-axis.
- the characteristic equation for
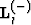 approximates the classical
eikonal equation.
approximates the classical
eikonal equation.
- The accuracy of the approximation increases with the number j.
The way to perform it is the expansion
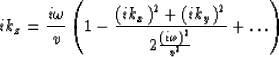
If we substitute the nth approximation of ikz into equation (95)
and return to the (r,t) domain, remembering the correspondence
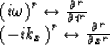
we get the equation which we looked for.
The first approximation:
| 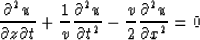 |
(97) |
yields to Jon Claerbout's famous 15-degree migration algorithm. With accordance
to the formula (24) (in Chapter 3), the characteristic equation which
corresponds to equation (97) is as follows:
| 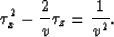 |
(98) |
It differs from classical eiconal's equation for isotropic medium.





Next: 9: INTEGRAL OPERATORS OF
Up: 8: CLASSIFICATION OF K-OPERATORS
Previous: Differential K-operators
Stanford Exploration Project
1/13/1998
![]() . Equation (95)
has the solution:
. Equation (95)
has the solution:
![]()
![]()
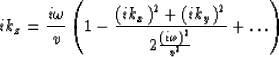
![]()