![]()
![]()
| |
(80) |
![]()
1. Absence of wave dispersion. Let the coefficient of the equation (80) be constant. After substitution
![]()
![]()
Looking for the solution in the form
![]()
![]()
![]()
2. Amplitude equivalence. This term means that while discontinuities propagate, amplitudes A change along rays s following the transport equation (see Chapter 4)
![]()
c=0
and![]()
3. Nonscattering vertical propagation. If in the amplitude-equivalent equation
| |
(81) |
![]()
II. Boundary conditions. There are few types of conditions that can be used for the wave-field continuation with the help of equation (80).
1. Mixed problem with boundary and initial conditions
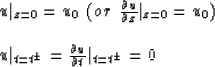
This problem has a unique and stable solution (in a restricted domain). It is
restricted at ![]() (for direct continuation) and
(for direct continuation) and ![]() (for inverse continuation) if h>0 and
(for inverse continuation) if h>0 and ![]() (or
(or ![]() ).
).
Representations of the solution:
![]() Finite-difference technique which can be applied
for any inhomogeneous media.
Finite-difference technique which can be applied
for any inhomogeneous media.
![]() Kirchhoff's type integral:
Kirchhoff's type integral:
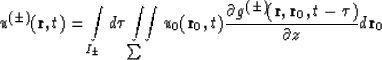 |
(82) |
where ![]() , I+ =(0, t), I(-) =(T-t, T),
, I+ =(0, t), I(-) =(T-t, T),
![]() -Green's function which is the solution
of the equation
-Green's function which is the solution
of the equation
| |
(83) |
For inhomogeneous media Green's function usually is unknown
(although one can calculate ray zero-approximation of
![]() ). In the case of wave equation
Green's function for homogeneous medium is
). In the case of wave equation
Green's function for homogeneous medium is
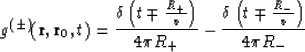 |
(84) |
![\begin{displaymath}
\begin{array}
{cl}
u^{(\pm)}({\bf r}, t) =
& {1\over 2\pi}\...
...bf D} u({\bf r}_0, t\mp{R\over v}) \Big ] d{\bf
r}_0\end{array}\end{displaymath}](img491.gif) |
(85) |
At big values of R the first term in square brackets can be neglected:
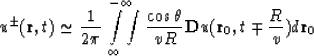 |
(86) |
These expressions are valid only in 3D case. In 2D case Green's function is
![\begin{displaymath}
g^+({\bf r}, {\bf r}_0, t) = {1\over 2\pi}\left[{H(t-{R_+\ov...
... {H(t-{R_-\over v})\over\sqrt{t^2 - ({R_-\over v})^2}}
\right]\end{displaymath}](img494.gif) |
(87) |
Inserting this into the equation (82) we obtain for the reverse continuation
![\begin{displaymath}
\begin{array}
{cl}
U^{(-)}({\bf r}, t) =
& {1\over \pi v}
...
...r v})\over
\sqrt{\tau-t+{2R\over v}}
}
\Big ]dx_0\end{array}\end{displaymath}](img495.gif) |
(88) |
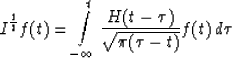 |
(89) |
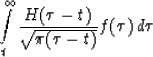
Let the field u0 (x0, t) contain a wave at t=t0.
The field u(-) will contain the wave at t = t0 -
R/v. Then the main contribution in the integral (88) is
made by the values of the field u0 at ![]() , that is,
, that is, ![]() .
.
Taking into account all these considerations and neglecting
the term with fast attenuating at ![]() , we
derive from equation (88):
, we
derive from equation (88):
| |
(90) |
![]() Spectral representation in (
Spectral representation in (![]() )-domain
(the wave equation, homogeneous media):
)-domain
(the wave equation, homogeneous media):
| |
(91) |
![]()
![]()
2. The Cauchy problem with respect to z in the ![]() domain
for the equation
domain
for the equation
| |
(92) |
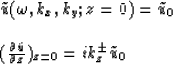
![]()
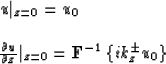
The natural way to stabilize Cauchy's problem is to cut off all frequencies at k2z < 0.
3. Reconstruction-type wave-field extrapolation. In this case we pose the conditions
![]()
| |
(93) |
There is only one reverse type regular continuation into homogeneous medium which satisfies the condition:
| u|z=0 =u0 | (94) |
![]()
In inhomogeneous media different conditions produce different solutions.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows an example of different solutions:
(a) is the reversed continuation of a single event at
shows an example of different solutions:
(a) is the reversed continuation of a single event at ![]() for
mixed conditions, and (b) for the Cauchy problem.
for
mixed conditions, and (b) for the Cauchy problem.
In Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) a we use reverse time -t instead of t (we can do it with
accordance with relation (51) in Chapter 5) because it promotes better understanding of
reflection-refraction pattern at the interface z=d. In reverse time we have the
usual process of wave propagation. Dashed lines show some ghost waves.
a we use reverse time -t instead of t (we can do it with
accordance with relation (51) in Chapter 5) because it promotes better understanding of
reflection-refraction pattern at the interface z=d. In reverse time we have the
usual process of wave propagation. Dashed lines show some ghost waves.