




Next: 4: CONNECTION WITH RAY
Up: 3: WHY DISCONTINUITIES?
Previous: Eikonal equation
The wave equation for elastic medium is a vector equation. It belongs to a class of equations
of the type:
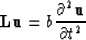
where  is a vector and
is a vector and 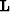 is a matrix operator:
is a matrix operator:
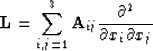
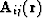 - a matrix.
- a matrix.
If we develop the same considerations as with the scalar case, we shall
obtain instead of equation (19) the vector equation
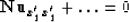
with a matrix
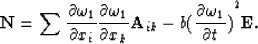
It is obvious that characteristics satisfy the equation
| 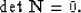 |
(23) |
In general, equation (23) has three solutions. This is due to the fact that in a continuous one-phase medium
where wave phenomena are described by second order equations,
only three types of body waves (not more, but eventually less!) may exist.
Let us check the Lame's equation (isotropic elasticity):
| 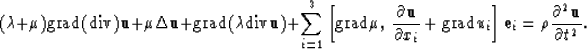 |
(24) |
We may omit the terms with first derivatives of u . So we have the system:
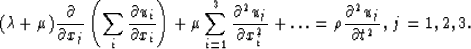
It is easy to derive the correspondent system of characteristic equations. The first
line is:
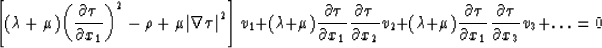
where 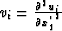 .
.
The matrix of the equation system may be written in the following form:
| 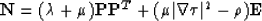 |
(25) |
where 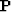 is a column vector with the components
is a column vector with the components 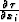 .
.
Let us prove that the vector 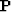 is an eigenvector of
is an eigenvector of 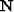 :
:
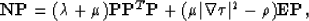
where 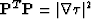 , so
, so
| ![\begin{displaymath}
\begin{array}
{lll}
{\bf NP} & = & [(\lambda + \mu)\vert\nab...
...mbda+2 \mu) \vert\nabla \tau\vert^2- \rho] {\bf P} .\end{array}\end{displaymath}](img185.gif) |
(26) |
Therefore, the first eigenvalue is:
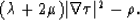
Let us consider a vector  :
:
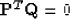
| 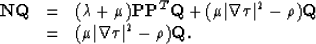 |
(27) |
The latter is valid for any vector 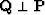 .Consequently, this eigenvalue is degenerated and it follows that
.Consequently, this eigenvalue is degenerated and it follows that
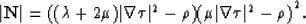
So we may satisfy the equation (19) in both cases:
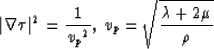
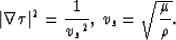
This means that in isotropic elastic media, there are only two types of body
waves which move with velocities vp and vs, respectively.
In the general case of anisotropic elastic media, there are three families
of characteristics and correspondently three body waves: quasi-P,
quasi-SV, and quasi-SH.
In Maxwell's equations of electrodynamics, there is only one characteristic
which propagates with the velocity of light.
We may say that geometrical seismics (as well as geometrical optics and
geometrical acoustics) describes the propagation of discontinuities.
We have studied here only the pure geometrical aspect of wave propagation,
but it will be shown that our results are also true for the amplitudes of waves.





Next: 4: CONNECTION WITH RAY
Up: 3: WHY DISCONTINUITIES?
Previous: Eikonal equation
Stanford Exploration Project
1/13/1998
![]()
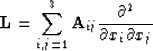
![]()
![]()
![]()
![]()
![]() is an eigenvector of
is an eigenvector of ![]() :
:
![]()
![]()
![]()
![]()
![]()
![]()