| |
(18) |
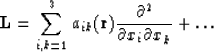
Let ![]() be a surface of arbitrary shape and let the values of
be a surface of arbitrary shape and let the values of
![]() and
and ![]() be given on the surface. Is this data
sufficient for the reconstruction of the unique solution of the
equation (18)? Does the Cauchy problem for equation (18)
with the initial data on
be given on the surface. Is this data
sufficient for the reconstruction of the unique solution of the
equation (18)? Does the Cauchy problem for equation (18)
with the initial data on ![]() have a unique solution? The answer will be
positive if it is possible to reconstruct all second derivatives on the surface
have a unique solution? The answer will be
positive if it is possible to reconstruct all second derivatives on the surface
![]() .
.
Let us introduce a system of functions ![]() ,with
,with ![]() and with the change of variables:
and with the change of variables:
![]()
On the surface ![]() all values
all values ![]() do vary. That means the given data allows one to calculate all mixed
derivatives
do vary. That means the given data allows one to calculate all mixed
derivatives ![]() and second derivatives
and second derivatives ![]() .Is it possible to calculate
.Is it possible to calculate ![]() ?
?
Let us express the derivatives with respect to the old variables through the derivatives with respect to the new variables, omitting terms that are not interesting for us, such as:
![]()
The equation (18) can be rewritten in the form:
| |
(19) |
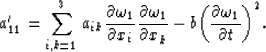
All terms denoted by dots are known on the surface ![]() ,so the only condition that supplies a possibility to determine
,so the only condition that supplies a possibility to determine ![]() is
is ![]() .If
.If ![]() , then the Cauchy problem is unsolvable. In this case, surface
, then the Cauchy problem is unsolvable. In this case, surface
![]() is a special one. And we call it a characteristic (or characteristic surface).
is a special one. And we call it a characteristic (or characteristic surface).
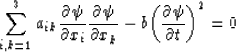 |
(20) |