




Next: Migration
Up: 6: WHY SO MANY
Previous: The method of time
Unfortunately equation (59) is valid only for common source and common receiver
gathers. Let us take, for instance, the common offset pattern in the 2D case :
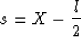
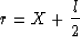
at fixed l. In this case we have datum
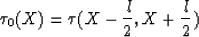
where 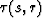 is the arrival time of a reflected wave propagating from source s to
receiver r. Then
is the arrival time of a reflected wave propagating from source s to
receiver r. Then
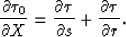
We can't separately determine values 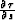 and
and
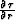 and, consequently, can't determine initial
conditions for eiconal
and, consequently, can't determine initial
conditions for eiconal  .We see that the reverse eikonal's continuation with datum
.We see that the reverse eikonal's continuation with datum 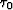 can't
reconstruct the true location of the seismic rays. The problem simplifies
greatly when l=0 (zero offset pattern). In this case incidence and
reflected rays coincide, and due to the principle of reciprocity,
can't
reconstruct the true location of the seismic rays. The problem simplifies
greatly when l=0 (zero offset pattern). In this case incidence and
reflected rays coincide, and due to the principle of reciprocity,
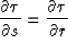
so
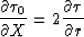
and
| 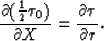 |
(61) |
This means that the solution 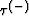 of equation (61) with initial condition
of equation (61) with initial condition
| 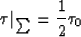 |
(62) |
will give the true ray pattern although the travel-times will be different.
This is not bad. Since the time of propagation from the reflector R to
surface 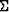 along the normal ray equals
along the normal ray equals 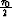 , the condition
, the condition
| 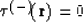 |
(63) |
determines the location of the reflector.
We could obtain the same result by solving the half-velocity eikonal equation
| 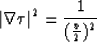 |
(64) |
with initial datum
| 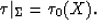 |
(65) |
Usually this scheme is obtained from some thought experiment (i.e., the exploding
reflector hypothesis). Let us find the forward eikonal's continuation
in the medium with velocity 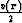 and initial condition
and initial condition
| 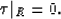 |
(66) |
This corresponds to a thought experiment with an impulsive source that is distributed along
the surface R at t=0).
It is easy to understand that the solution 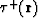 of this
problem will coincide on the surface
of this
problem will coincide on the surface 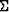 with
with 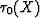 . It is clear
that the reverse eikonal's continuation
. It is clear
that the reverse eikonal's continuation 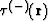 of
of 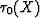 in a medium with half-velocity has the isochron
in a medium with half-velocity has the isochron 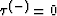 on the surface R.
on the surface R.





Next: Migration
Up: 6: WHY SO MANY
Previous: The method of time
Stanford Exploration Project
1/13/1998
![]()
![]()
![]()
![]()
![]()
![]()