




Next: Zero-offset case
Up: 6: WHY SO MANY
Previous: 6: WHY SO MANY
During World War II the Soviet geophysicist J. Riznichenko
proposed the following method for reconstruction of a reflector in a
medium with a given velocity 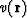 .Let the source be located at point
.Let the source be located at point  and let
and let 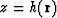 be a surface that shows the location of a reflector R.
In a medium D between surfaces
be a surface that shows the location of a reflector R.
In a medium D between surfaces 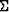 and R two eikonals can be
introduced:
and R two eikonals can be
introduced:
- eikonal of the direct wave:
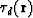
- eikonal of the wave reflected from R:
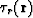 .
.
Both eikonals satisfy the eikonal equation
| 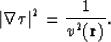 |
(53) |
The initial condition for 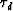 is
is
| 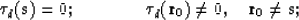 |
(54) |
initial condition for 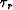 is
is
| 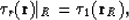 |
(55) |
where
| 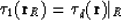 |
(56) |
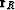 are curvilinear coordinates on the surface R.
are curvilinear coordinates on the surface R.
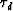 and
and 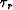 are determined as the direct eikonal's continuations.
are determined as the direct eikonal's continuations.
It is by definition that eikonals 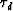 and
and 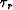 have the same values on
the reflector R:
have the same values on
the reflector R:
| 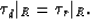 |
(57) |
In fact the surface R is a geometrical collection of points  that
satisfies equation
that
satisfies equation
| 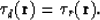 |
(58) |
We suggest that travel-times 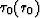 for a common source are
given on the surface
for a common source are
given on the surface 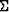 . Since the velocity-function
. Since the velocity-function 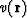 is proposed
to be known, we can determine the reverse eikonal continuation
is proposed
to be known, we can determine the reverse eikonal continuation 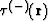 .Both functions
.Both functions 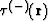 and
and 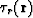 :
:
- satisfy the same equation (53)
- coincide with
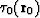 on
on 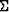
- approach the surface
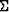 from below.
from below.
This means that
| 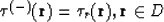 |
(59) |
and the reflector's location is determined by
| 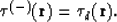 |
(60) |
In fact, Riznichenko proposed not only this theoretical scheme but also a
graphical scheme. Huygens principle founded method of reconstructing
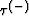 and
and 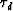 in the 2D case. Nowadays this second scheme has lost its
significance since we have a great deal of different computer-flexible
techniques to solve equation (53). Due to the principle
of reciprocity, absolutely the same scheme works when, instead of
in the 2D case. Nowadays this second scheme has lost its
significance since we have a great deal of different computer-flexible
techniques to solve equation (53). Due to the principle
of reciprocity, absolutely the same scheme works when, instead of 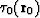 , we
have
, we
have 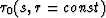 : travel-times for common receiver patterns with source location s.
: travel-times for common receiver patterns with source location s.
It is easy to extend this technique to converted waves PS or SP: in this
case we must use different velocities for reconstructing 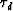 and
and
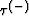 .
.





Next: Zero-offset case
Up: 6: WHY SO MANY
Previous: 6: WHY SO MANY
Stanford Exploration Project
1/13/1998
![]() .Let the source be located at point
.Let the source be located at point ![]() and let
and let ![]() be a surface that shows the location of a reflector R.
In a medium D between surfaces
be a surface that shows the location of a reflector R.
In a medium D between surfaces ![]() and R two eikonals can be
introduced:
and R two eikonals can be
introduced:
![]() and
and ![]() have the same values on
the reflector R:
have the same values on
the reflector R:
![]() and
and
![]() .
.