




Next: 7: GEOMETRICAL PROBLEMS OF
Up: 6: WHY SO MANY
Previous: Zero-offset case
Since discontinuities of the wave field 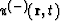 move with eikonal
move with eikonal 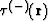 it is easy to reconstruct the reflector's location (without picking seismic
events) with the help of an operator
it is easy to reconstruct the reflector's location (without picking seismic
events) with the help of an operator 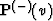 . In the case of common source patterns:
. In the case of common source patterns:
| 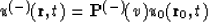 |
(67) |
and the image of the reflector is a correspondent discontinuity of the field
| 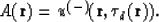 |
(68) |
This formula follows directly from equation (60). In order to get a better
understanding, let us propose that the discontinuity of the field
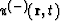 has an order q.
If we differentiate the field
has an order q.
If we differentiate the field 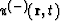 q+1 times, this discontinuity
will become a
q+1 times, this discontinuity
will become a 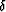 -function:
-function:
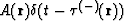 .If instead of t we substitute
.If instead of t we substitute 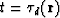 , then the support of
, then the support of
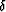 -function will satisfy equation 60.
-function will satisfy equation 60.
In the zero offset case
| 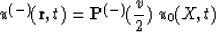 |
(69) |
where u0(x,t) is a set of seismic records with s=r=X. The image of the
reflector coincides with the discontinuity of the field
| 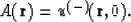 |
(70) |
In both cases depth migration consists of two steps:
- reverse wave continuation
- imaging.
This scheme is applicable only in the cases of common source, common receiver,
or zero offset gathers. It does not mean that migration cannot be performed
for other patterns. On the contrary: we shall show that migration may be done
for any arbitrary pattern. But in the previously mentioned gathers, it may be
done with these two steps: wave field continuation and imaging. I don't take into
consideration possible approximate approaches.
Now we can answer the question: why do we have so many algorithms of migration?
For this purpose, we can use any kinematically-equivalent operation:
all of them are useful for imaging reflectors.
Classical time migration is a result of the substitution 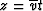 :
:
| 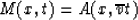 |
(71) |
where 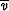 is an average velocity along a vertical line and
is an average velocity along a vertical line and
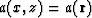 .
.





Next: 7: GEOMETRICAL PROBLEMS OF
Up: 6: WHY SO MANY
Previous: Zero-offset case
Stanford Exploration Project
1/13/1998
![]() has an order q.
If we differentiate the field
has an order q.
If we differentiate the field ![]() q+1 times, this discontinuity
will become a
q+1 times, this discontinuity
will become a ![]() -function:
-function:
![]() .If instead of t we substitute
.If instead of t we substitute ![]() , then the support of
, then the support of
![]() -function will satisfy equation 60.
-function will satisfy equation 60.
![]() :
: