Ray method

In the framework of the ray method one looks for a solution of an equation using the following representation of a wave field:

 

$${\bf u}({\bf r},t)={\rm Re} \sum ^{\infty}_{n=0} {\bf U}_{n}( {\bf r}) f_{n}(t-\tau ({\bf r}))$$ (28)

where ${\bf U}_{n}({\bf r})$ are complex vector amplitudes: ${\bf U}_n=U^{(1)}_n+U^{(2)}_n+U^{(3)}_n$, f_n(t) are ``complex forms'' which satisfy the relation  

$$f_{n-1}(t)={d\over dt} f_{n}(t)={\bf D} f_{n}(t).$$ (29)

If we put expression (28) into the equation  

$${\bf L} {\bf u} ({\bf r},t)=\rho {\partial ^{2}u \over \partial t^{2}}$$ (30)

(it can be, for instance, Lame's equation; see Chapter 3, equation (24)), we derive, after some manipulating, that function $\tau ({\bf r})$ satisfy eiconal's equation  

$${\vert\Delta \tau \vert}^{2}= {1 \over v^{2}_{Q}}$$ (31)

(Q stands for P or S), and complex amplitudes satisfy the recurrent relations:  

$${\bf N}{\bf U}_{n}={\bf M}{\bf U}_{n-1}-{\bf L}{\bf U}_{n-2}, {\:}{\:}n=0, 1, 2, \ldots, {\:}{\:}{\bf U}_{-2}={\bf U}_{-1}=0,$$ (32)

where ${\bf L}$ is the same operator as in equation (30), ${\bf N}$ is the same matrice that is in Chapter 3 (see equation (23)), and ${\bf M}$ is a first order differential operator:  

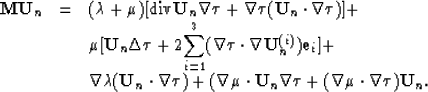$$\begin{array} {lll} {\bf M}{\bf U}_n & = & (\lambda+\mu)[\hb... ...bla \tau + (\nabla \mu \cdot \nabla \tau) {\bf U}_n.\end{array}$$ (33)

We see that ``ray waves'' propagate with the same eiconal as discontinuities. It is not accidental because standard discontinuities satisfy the same relation (29) as ``complex forms'' f_n(t).

Moreover, if a source function has a beginning at the t=0 (as it usually occurs), then the solution of the equation (30) will inevitably have discontinuities that propagate with eiconal's satisfying equation (31). This means that all complex forms f_n(t) must have a discontinuity at the point t=0. Therefore, despite the choice of a complex form f₀(t), any ``ray series'' descriptions of the wave field are equivalent in the sense that was introduced earlier.

Of course, a choice of f₀(t) influences accuracy of wave field approximation behind the wave front $\tau = \tau ({\bf r})$, but in any case, convergence of the series (28) can be guaranteed only in a neighborhood of wave front (Babich, 1961).

If f₀(t)=R_q<<933>>0(t) then series (28) represents ordinary Tailor's expansion in a neighborhood of the front (in the case of the ``weak discontinuity'', q₀=2).

In the general case

$$f_{0}(t) \stackrel{q_{0}}{\sim } R_{q_{0},0} (t)+iR_{q_{0},1}(t)$$

where q₀ can vary depending on the location of the point ${\bf r}$.We observe this dependence in a neighborhood of caustics and other special domains. But in this case we have to learn how to manipulate with discontinuities of noninteger order.

We see that usage of discontinuities is absolutely equivalent to ray series approach. Both approaches give the same geometrical law of wave propagation and the same behavior of wave amplitudes during propagation.

If the senior discontinuity has the order q₀, then the equivalence of the order q₀ corresponds to the zero-approximation of ray series; equivalence of the order q₀+1 corresponds to the first-order ray-series approximation and so on.

Usually the value of q₀ does not matter. So it will be convenient to write $f_{1}(t) \stackrel{(k)}{\sim } f_{2} (t)$, if there is such an order q₀ that $f_{1}(t) \stackrel{q_{0}+r}{\sim } f_{2} (t)$for all $r=0,1, \ldots , k$, but not for r<0. With this agreement, zero-approximation corresponds to (0)-equivalence, first-order ray-series approximation corresponds to (1)-equivalence, and so on. Usually we shall omit symbol (0) (so $\sim \equiv \stackrel{(0)}{\sim }$).