Concatenating the two operators

Let ${\bf w^0}$ and ${\bf r^0}$ be some initial estimations of the wavelet and reflectivity sequence respectively. The data residuals can be described by

$$\begin{array} {rcl} {\bf \Delta t^0} & = & {\bf t} - {\bf w... ...r^0 \ast \Delta w} + {\bf \Delta w \ast \Delta r}, \end{array}$$

which can be linearized for small ${\bf \Delta w}$ and ${\bf \Delta r}$: 

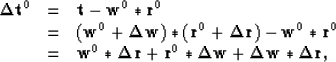
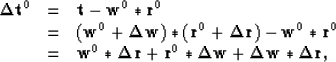
$${\bf \Delta t^0} = {\bf w^0 \ast \Delta r} + {\bf r^0 \ast \Delta w}.$$ (15)

By applying the ${\bf P_{w^0}}$ operator to equation (15), we get

$${\bf \Delta r} = {\bf P_{w^0} \{ \Delta t \}} - {\bf P_{w^0} \{ r^0 \ast \Delta w \}}.$$

If the sequence ${\bf r^0}$ is sufficiently sparse, the last term will involve the correlation between ${\bf w^0}$ and ${\bf \Delta w}$, which we can expect to be somewhat uncorrelated. The same reasoning can be applied to the operator ${\bf Q_{r^0}}$, resulting in the following recursion for reflectivities and waveform

$$\begin{eqnarray} {\bf r^i} & = & {\bf r^{i-1}} + {\bf P_{w^{i-1}} \{ \Delta t^{i... ...w^i} & = & {\bf w^{i-1}} + {\bf P_{r^{i-1}} \{ \Delta t^{i-1} \}}.\end{eqnarray}$$ (16) (17)

If we start the process with an initial estimation for the wavelet, then the initial estimation for the reflectivity sequence can be obtained when we apply ${\bf P_{w^0}}$ to the trace. As in most non-linear processes, the final solution depends on the initial choice for the wavelet. In all the next examples I used the minimum-phase wavelet corresponding to the smoothed spectrum of the trace as an initial estimation of the wavelet. Although the method has always converged for several different selections of the starting wavelet, an analytical proof that assures its convergence has not yet been derived.