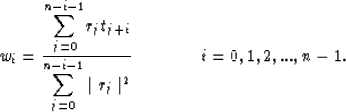Next: Concatenating the two operators
Up: SIMULTANEOUS ESTIMATION OF WAVELET
Previous: SIMULTANEOUS ESTIMATION OF WAVELET
Although the convolution in equation (1) is commutative,
the different spectra of 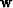 and
and  disallow us from
using the same operator defined in equation (2) to retrieve
the wavelet when the reflectivity sequence is completely known.
However, if we start again from the ideal case of a sparse reflectivity
sequence, it is possible to define an operator
disallow us from
using the same operator defined in equation (2) to retrieve
the wavelet when the reflectivity sequence is completely known.
However, if we start again from the ideal case of a sparse reflectivity
sequence, it is possible to define an operator 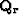 that retrieves the
exact wavelet:
that retrieves the
exact wavelet:
| 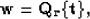 |
(12) |
where the operator 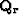 is defined according to
is defined according to
| 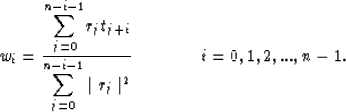 |
(13) |
This operator corresponds to a normalized correlation that
properly handles edge effects because the norm in the denominator
is evaluated over only the active part of r.
A similar approach to the one described for reflectivity estimation
can be taken for the wavelet estimation in the case of a non-sparse
known reflectivity sequence. The iterative process is then described
by
| 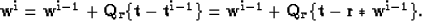 |
(14) |





Next: Concatenating the two operators
Up: SIMULTANEOUS ESTIMATION OF WAVELET
Previous: SIMULTANEOUS ESTIMATION OF WAVELET
Stanford Exploration Project
1/13/1998
![]() and
and ![]() disallow us from
using the same operator defined in equation (2) to retrieve
the wavelet when the reflectivity sequence is completely known.
However, if we start again from the ideal case of a sparse reflectivity
sequence, it is possible to define an operator
disallow us from
using the same operator defined in equation (2) to retrieve
the wavelet when the reflectivity sequence is completely known.
However, if we start again from the ideal case of a sparse reflectivity
sequence, it is possible to define an operator ![]() that retrieves the
exact wavelet:
that retrieves the
exact wavelet: