Next: Building a more complex
Up: DECONVOLUTION WITH A KNOWN
Previous: DECONVOLUTION WITH A KNOWN
If we consider the simple case in which  is a sufficiently
sparse series (so that the number of samples between any two adjacent
non-zero-valued samples is at least equal to the number of
samples of the wavelet, i.e. Lw),
it is possible to devise a simple operator to retrieve
is a sufficiently
sparse series (so that the number of samples between any two adjacent
non-zero-valued samples is at least equal to the number of
samples of the wavelet, i.e. Lw),
it is possible to devise a simple operator to retrieve  :
:
| 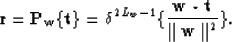 |
(2) |
The symbol stands for correlation, while the operator
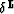 is defined as follows:
The result of
is defined as follows:
The result of
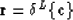
is given by
where
When the series  is still sparse but the temporal
distance between non-vanishing-samples is larger than the minimum
distance still resolvable by the wavelet (that is
is still sparse but the temporal
distance between non-vanishing-samples is larger than the minimum
distance still resolvable by the wavelet (that is ![$ dt \ge 1/[2f]$](img12.gif) , where f is the highest frequency component of the wavelet), the
operator in equation (2) will not give the exact solution.
Here however, an exact solution can still be obtained through
an iterative process. Let's consider equation (2) as
the zero-order approximation
, where f is the highest frequency component of the wavelet), the
operator in equation (2) will not give the exact solution.
Here however, an exact solution can still be obtained through
an iterative process. Let's consider equation (2) as
the zero-order approximation  to the time series
to the time series  :
:
|  |
(3) |
The residual between the original trace and the trace predicted
by this zero-order approximation for the reflectivity will be
| 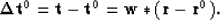 |
(4) |
Because the operator 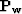 in equation (2) is an approximation
to the inverse of the convolution by
in equation (2) is an approximation
to the inverse of the convolution by 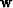 , we can apply it
to equation (4) to get a zero-order approximation to
, we can apply it
to equation (4) to get a zero-order approximation to
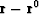 :
:
| 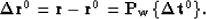 |
(5) |
Therefore, the first-order approximation for the reflectivity series
will be
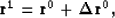
and in general
| 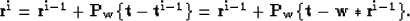 |
(6) |
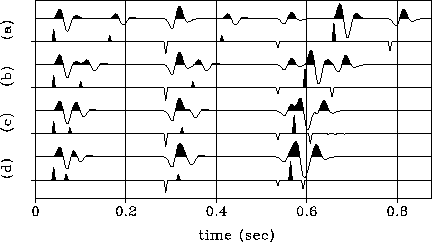
In Figure 1 this iterative process is applied to
a synthetic trace whose original reflectivity series is
comprised of sparse spikes. The distance between some of
the spikes is successively decreased to show how the
relaxation of the sparseness condition affects
the convergence of the method. Except for (c), the
exact solution was reached in a few number of iterations, even
when the separation between adjacent spikes is reduced to
one third of the wavelet size. Because in (c)
the exact solution was not reached within a finite number
of iterations (though an extremely close solution was
found after a few iterations), it will be necessary to improve
the basic operator Pw if we intend to apply the method to
more complex time series.
sparse
Figure 1 The iterative process described by equation (6)
is applied to four synthetic traces. The traces differ
only in the distance between some of the spikes of
the associated reflectivity series. (a) When the
distance between spikes is around 1.5 times the wavelet's size
the exact reflectivities are retrieved on the 0-order iteration
(that is, equation 2). As the distance between
some of the spikes decreases, the number of iterations necessary
to get the exact solution increases: 1 iteration in (b)
and 8 iterations in (d). Although (c) has a fast convergence
(the sixth iteration is shown), the exact solution is not
reached, as we can see by the small residuals
beyond 0.6 seconds.






Next: Building a more complex
Up: DECONVOLUTION WITH A KNOWN
Previous: DECONVOLUTION WITH A KNOWN
Stanford Exploration Project
1/13/1998
![]()
![]()
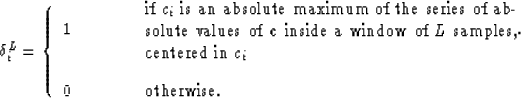
![]() is still sparse but the temporal
distance between non-vanishing-samples is larger than the minimum
distance still resolvable by the wavelet (that is
is still sparse but the temporal
distance between non-vanishing-samples is larger than the minimum
distance still resolvable by the wavelet (that is ![]() , where f is the highest frequency component of the wavelet), the
operator in equation (2) will not give the exact solution.
Here however, an exact solution can still be obtained through
an iterative process. Let's consider equation (2) as
the zero-order approximation
, where f is the highest frequency component of the wavelet), the
operator in equation (2) will not give the exact solution.
Here however, an exact solution can still be obtained through
an iterative process. Let's consider equation (2) as
the zero-order approximation ![]() to the time series
to the time series ![]() :
:
![]() in equation (2) is an approximation
to the inverse of the convolution by
in equation (2) is an approximation
to the inverse of the convolution by ![]() , we can apply it
to equation (4) to get a zero-order approximation to
, we can apply it
to equation (4) to get a zero-order approximation to
![]() :
: ![]()