Blocky velocity inversion by hybrid norm

Regularization by the Helix Derivative Operator

Now we consider the helix derivative (Claerbout, 1997) as a regularization operator. Figure 5 shows the results of using the $L2$ norm, and Figure 6 shows the results of using the hybrid norm. In this case, we see a dramatic difference between the two results. In the hybrid norm case, we can see the beginnings of blockiness, but only in one direction (toward the right). The reason for this asymmetry is that using an L1-like norm is similar to applying the regularization only once. On the other hand, we do not see this effect in the $L2$ norm results, because the regularization in that norm is similar to applying the forward and the adjoint of an operator, which is a symmetric procedure.

l2-lab27
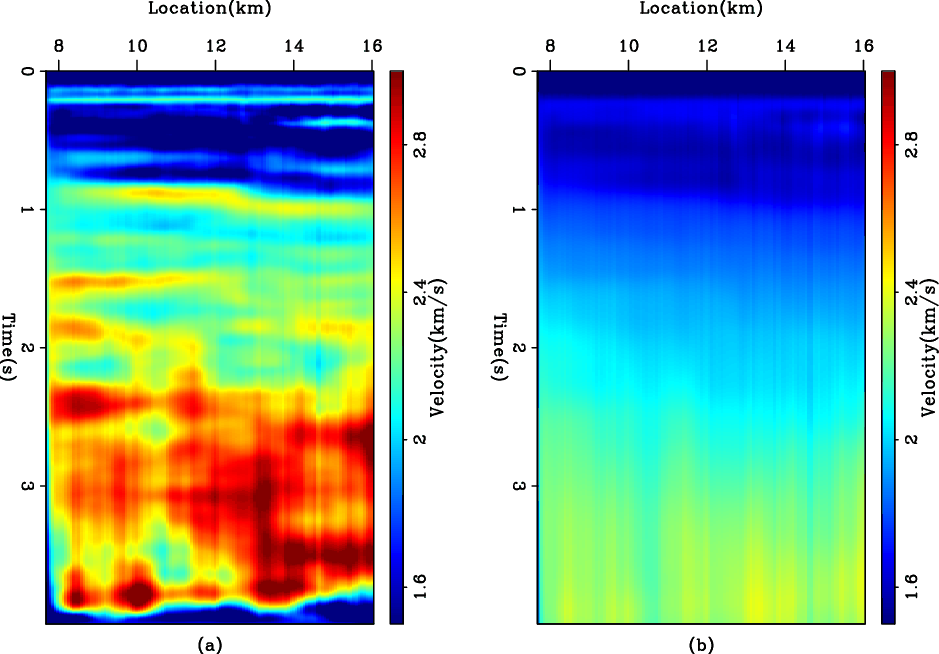
Figure 5. The WG dataset. (a) The interval velocity estimated by using the helix derivative operator as a regularization in the $L2$ norm. (b) The reconstructed RMS velocity.

hbe-lab29
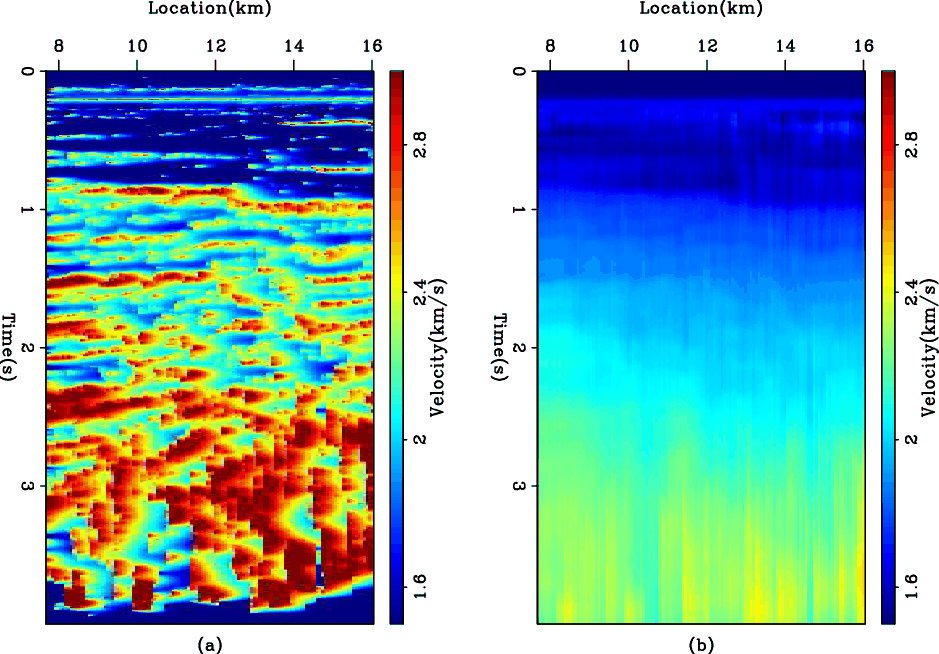
Figure 6. The WG dataset. (a) The interval velocity estimated by using the helix derivative operator as a regularization in the hybrid norm. (b) The reconstructed RMS velocity.

Blocky velocity inversion by hybrid norm